
| A. | [-4,-2] | B. | [-2,-1] | C. | [-4,-1] | D. | $[{-1,-\frac{1}{2}}]$ |
分析 由题意设出椭圆${x^2}+\frac{y^2}{4}=1$的某弦的两个端点分别为P(x1,y1),Q(x2,y2),中点为M(x0,y0),把P、Q的坐标代入椭圆方程,作差得到PQ的斜率与AB中点坐标的关系得答案.
解答 解:设椭圆${x^2}+\frac{y^2}{4}=1$的某弦的两个端点分别为P(x1,y1),Q(x2,y2),中点为M(x0,y0),
则${{x}_{1}}^{2}+\frac{{{y}_{1}}^{2}}{4}=1$,${{x}_{2}}^{2}+\frac{{{y}_{2}}^{2}}{4}=1$,
两式作差可得:${{x}_{1}}^{2}-{{x}_{2}}^{2}=-\frac{{{y}_{1}}^{2}}{4}+\frac{{{y}_{2}}^{2}}{4}$,
即$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}=-\frac{4({x}_{1}+{x}_{2})}{{y}_{1}+{y}_{2}}=-\frac{4{x}_{0}}{{y}_{0}}$=$-\frac{4×\frac{1}{2}}{{y}_{0}}=-\frac{2}{{y}_{0}}$,
由题意可知,$\frac{1}{2}≤$y0≤1,
∴k=$-\frac{2}{{y}_{0}}$($\frac{1}{2}≤$y0≤1),则k∈[-4,-2].
故选:A.
点评 本题考查椭圆的简单性质,训练了“中点弦”问题的求解方法,属中档题.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2] | B. | $({0,\frac{1}{2}}]$ | C. | $[{\frac{1}{2},2}]$ | D. | (0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
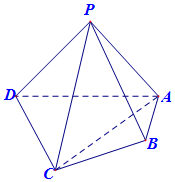 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=$\sqrt{5}$.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=$\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com