考点:直线与平面垂直的性质
专题:空间位置关系与距离
分析:(Ⅰ)先利用面面垂直的判定定理证明出平面A1AC⊥平面ABC,进而证明出BC⊥AC1,同理根据菱形的性质证明出A1C⊥AC1,利用线面垂直的判定定理证明出AC1⊥平面A1CB,最后根据线面垂直的性质证明出AC1⊥BA1.
(Ⅱ)分别求出VA1B1C1-ABC和VA1-ABC最后作差即可.
解答:
(Ⅰ)证明:∵A
1在底面ABC上的射影恰为AC的中点D,
∴A
1D⊥平面ABC,
∵A
1D?平面A
1AC,
∴平面A
1AC⊥平面ABC,
∵BC⊥AC,平面A
1AC∩平面ABC=AC,
∴BC⊥平面A
1AC,
∵AC
1?平面A
1AC,
∴BC⊥AC
1,
∵四边形ACC
1A
1为平行四边形,AA
1=AC,
∴四边形ACC
1A
1为菱形,
∴A
1C⊥AC
1,
∵A
1C?平面A
1CB,BC?平面A
1CB,A
1C∩BC=C,
∴AC
1⊥平面A
1CB,
∵BA
1?平面A
1CB,
∴AC
1⊥BA
1.
(Ⅱ)∵
VA1-ABC=
S
△ABC•A
1D=
×
×2×2×
=
.
VA1B1C1-ABC=S
△ABC•A
1D=
×2×2×
=2
.
∴
VA1-BCC1B1=
VA1B1C1-ABC-
VA1-ABC=2
-
=
.
点评:本题主要考查了线面垂直的判定定理的应用,和棱柱体积的计算.考查了学生空间观察能力和实际运算能力.

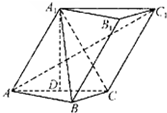 已知三棱柱ABC-A1B1C1中,∠BCA=90°,AA1=AC=BC=2,A1在底面ABC上的射影恰为AC的中点D.
已知三棱柱ABC-A1B1C1中,∠BCA=90°,AA1=AC=BC=2,A1在底面ABC上的射影恰为AC的中点D.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案 如图,△A′O′B′是水平放置的△AOB由斜二测画法得到的直观图,则原△AOB的三边及中线AM中,最长的线段是( )
如图,△A′O′B′是水平放置的△AOB由斜二测画法得到的直观图,则原△AOB的三边及中线AM中,最长的线段是( )