
| A. | 3 | B. | 5 | C. | 8 | D. | 11 |
分析 根据题中的对应法则,算出f1(8)、f2(8)、f3(8)、f4(8)的值,从而发现规律fk+3(8)=fk(8)对任意k∈N*成立,由此即可得到答案.
解答 解:∵82+1=65,∴f1(8)=f(8)=6+5=11,
同理,由112+1=122得f2(8)=1+2+2=5;由52+1=26,得f3(8)=2+6=8,
可得f4(8)=6+5=11=f1(8),f5(8)=f2(8),…,
∴fk+3(8)=fk(8)对任意k∈N*成立
又∵2016=3×672,
∴f2016(8)=f2013(8)=f2000(8)=…=f3(8)=8.
故选:C.
点评 本题给出函数fk(x)的对应法则,求f2016(8)的值.着重考查了函数的定义、数列的递推公式和进行简单的合情推理等知识,属于基础题.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:解答题
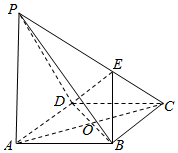 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,PA=4,AC=2$\sqrt{3}$,BD=2,又点E在侧棱PC上,且PC⊥平面BDE.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,PA=4,AC=2$\sqrt{3}$,BD=2,又点E在侧棱PC上,且PC⊥平面BDE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com