
分析 二面角α-l-β中,PA⊥α,PB⊥β,PO⊥l,PA=a,PB=$\sqrt{2}a$,PO=2a,连结AO、BO,则∠AOB是二面角的平面角,由此能求出结果.
解答 解:如图,二面角α-l-β中,PA⊥α,PB⊥β,PO⊥l,
PA=a,PB=$\sqrt{2}a$,PO=2a
连结AO、BO,则∠AOB是二面角的平面角,
∵AO⊥l,BO⊥l,PO⊥l,∴AOBP是平面图形,
∴∠POA=30°,∠POB=45°,
如图一,∠AOB=∠POA+∠POB=30°+45°
=75°.
如图二,∠AOB=180°-(∠POB-∠POA)
=180°-(45°-30°)=165°.
故答案为:75°或165°.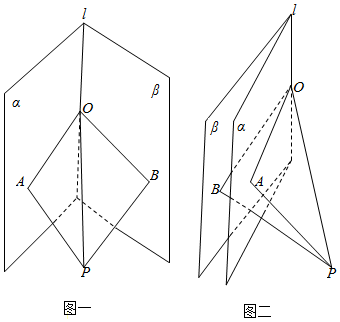
点评 本题主要考查了二面角的平面角及求法,求二面角,关键是构造出二面角的平面角,常用的方法有利用三垂线定理和通过求法向量的夹角,然后再将其转化为二面角的平面角.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
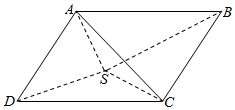 如图,四边形 A BCD为平行四边形,且SD=2,SC=DC=AS=AD=$\sqrt{2}$,平面 ASD⊥平面SDC.
如图,四边形 A BCD为平行四边形,且SD=2,SC=DC=AS=AD=$\sqrt{2}$,平面 ASD⊥平面SDC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
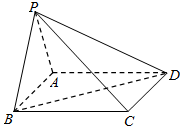 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,面PAB⊥底面ABCD,PB=1,且∠PBA=60°
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,面PAB⊥底面ABCD,PB=1,且∠PBA=60°查看答案和解析>>
科目:高中数学 来源: 题型:解答题
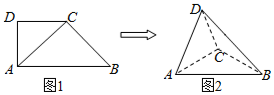 如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AD=CD=$\frac{1}{2}$AB=2.将△ADC沿AC折起,使平面ADC⊥平面ABC,得到如图2所示的几何体D-ABC
如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AD=CD=$\frac{1}{2}$AB=2.将△ADC沿AC折起,使平面ADC⊥平面ABC,得到如图2所示的几何体D-ABC查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 5 | C. | 8 | D. | 11 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com