
 为了解某地脐橙种植情况,调研小组在该地某脐橙种植园中随机抽出30棵,每棵挂果情况编成如图所示的茎叶图(单位:个):若挂果在175个以上(包括175)定义为“高产”,挂果在175个以下(不包括175)定义为“非高产”.
为了解某地脐橙种植情况,调研小组在该地某脐橙种植园中随机抽出30棵,每棵挂果情况编成如图所示的茎叶图(单位:个):若挂果在175个以上(包括175)定义为“高产”,挂果在175个以下(不包括175)定义为“非高产”.分析 (1)根据茎叶图,有“高产”12棵,“非高产”18棵,用分层抽样的方法,选中的“高产”有2棵,“非高产”有3棵,由此能求出至少有一棵是“高产”的概率.
(2)依题意,从所有脐橙果树中抽取一棵是“高产”的概率是$\frac{2}{5}$,ξ服从二项分布$B(3,\frac{2}{5})$,由此能求出ξ的分布列和数学期望.
解答 解:(1)根据茎叶图,有“高产”12棵,“非高产”18棵,
用分层抽样的方法,每棵被抽中的概率是$\frac{5}{30}=\frac{1}{6}$…(2分)
所以选中的“高产”有$12×\frac{1}{6}=2$棵,“非高产”有$18×\frac{1}{6}=3$棵,
用事件A表示至少有一棵“高产”被选中,
则$P(A)=1-\frac{C_3^2}{C_5^2}=1-\frac{3}{10}=\frac{7}{10}$,
因此至少有一棵是“高产”的概率是$\frac{7}{10}$.…(4分)
(2)依题意,抽取30棵中12棵是“高产”,
所以抽取一棵是“高产”的频率为$\frac{12}{30}=\frac{2}{5}$…(5分)
频率当作概率,那么从所有脐橙果树中抽取一棵是“高产”的概率是$\frac{2}{5}$,
又因为所取总体数量较多,抽取3棵可看成进行3次独立重复试验,
所以ξ服从二项分布$B(3,\frac{2}{5})$…(6分)
ξ的取值为0,1,2,3,
$P(ξ=0)=C_3^0{(1-\frac{2}{5})^3}=\frac{27}{125}$,
P(ξ=1)=${C}_{3}^{1}•\frac{2}{5}•(1-\frac{2}{5})^{2}$=$\frac{54}{125}$,
P(ξ=2)=${C}_{3}^{2}(\frac{2}{5})^{2}(1-\frac{2}{5})$=$\frac{36}{125}$,
$P(ξ=3)=C_3^3{(\frac{2}{5})^3}=\frac{8}{125}$…(9分)
所以ξ的分布列如下:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{27}{125}$ | $\frac{54}{125}$ | $\frac{36}{125}$ | $\frac{8}{125}$ |
点评 本题考查茎叶图、分层抽样的应用,考查离散型随机变量的分布列、数学期望的求法,是中档题,解题时要认真审题,注意二项分布的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x1)<0,f(x2)<0 | B. | f(x1)<0,f(x2)>0 | C. | f(x1)>0,f(x2)>0 | D. | f(x1)>0,f(x2)<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 人体的脂肪含量与年龄之间没有相关关系 | |
| B. | 汽车的重量和汽车每消耗1L汽油所行驶的平均路程负相关 | |
| C. | 吸烟量与健康水平正相关 | |
| D. | 气温与热饮销售好不好正相关 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
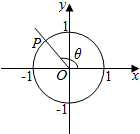
| A. | -$\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | -$\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD是直角梯形,∠BAD=∠ADC=90°,E为CB的中点,AB=PA=AD=2CD,则PA与平面PDE所成的角的正弦值为( )
如图,四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD是直角梯形,∠BAD=∠ADC=90°,E为CB的中点,AB=PA=AD=2CD,则PA与平面PDE所成的角的正弦值为( )| A. | $\frac{\sqrt{22}}{22}$ | B. | $\frac{\sqrt{22}}{11}$ | C. | $\frac{3\sqrt{22}}{22}$ | D. | $\frac{2\sqrt{22}}{11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 上春晚次数x(单位:次) | 1 | 2 | 4 | 6 | 8 |
| 粉丝数量y(单位:万人) | 5 | 10 | 20 | 40 | 80 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com