
| A�� | ����С���˷�ԭ���µõ��Ļع�ֱ�߷���$\widehat{y}$=0.52x+$\widehat{a}$����y��x��������ع�ϵ | |
| B�� | �в�ƽ����ԽС��ģ�ͣ���ϵ�Ч��Խ�� | |
| C�� | �ڲв�ͼ�У��в��ȽϾ��ȵ�����ˮƽ�Ĵ�״�����ڣ�˵��ѡ�õ�ģ�ͱȽϺ��� | |
| D�� | �����ָ��R2���̻��ع�Ч����R2ԽС˵�����Ч��Խ�� |
���� ������������ģ��Ч���û��ļ������ֱ������ָ�����в�ƽ���ͺ����ϵ����ֻ�вв�ƽ����ԽСԽ�ã������Ķ���Խ��Խ�ã�
��� �⣺����С���˷�ԭ���µõ��Ļع�ֱ�߷���$\widehat{y}$=0.52x+$\widehat{a}$��b=0.52��0����y��x��������ع�ϵ����ȷ��
�в�ƽ����ԽС��ģ�ͣ���ϵ�Ч��Խ�ã���ȷ��
���òв�ͼ�ж�ģ�͵����Ч�����в��ȽϾ��ȵ�����ˮƽ�Ĵ�״�����У�˵��������ģ�ͱȽϺ��ʣ���״����Ŀ���Խխ��˵��ģ�͵���Ͼ���Խ�ߣ�����ȷ��
���ָ��R2ȡֵԽ��˵���в�ƽ����ԽС��ģ�͵����Ч��Խ�ã��ʲ���ȷ��
��ѡ��D��
���� ���⿼�������������֮����ع�ϵ�ķ�����Ҫ��֪����������֮����йػ��صľ�ȷ�Ŀ��ų̶ȣ�ֻ�����ö����Լ�����йؼ��㣬���������жϣ����ڻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {1} | B�� | {2} | C�� | 1 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 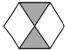 | B�� | 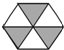 | C�� |  | D�� | 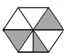 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{��}{4}$ | B�� | $\frac{3��}{4}$ | C�� | $\frac{��}{3}$ | D�� | $\frac{2��}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {1��2} | B�� | {2��3} | C�� | {1��2��3} | D�� | {0��1��2} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com