Question

17．已知定义在R上的偶函数f（x）的周期为4，当x∈[0，2]时，f（x）=|2^x-2|，若函数g（x）=f（x）-|（$\frac{1}{2}$）^x-$\frac{1}{2}$|，则当x∈[-2016，2016]，时，函数g（x）的零点个数是（　　）

• A． 1003
• B． 2016
• C． 4032
• D． 2017

Answer 1

分析 根据函数的周期性和奇偶性求出在一个周期内的解析式，作出两个函数的图象，利用数形结合进行求解即可．

解答 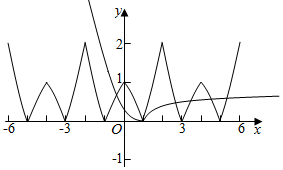解：∵定义在R上的偶函数f（x）的周期为4，当x∈[0，2]时，f（x）=|2^x-2|，
∴当x∈[-2，0]，则-x∈[0，2]，
则f（-x）=|2^-x-2|=f（x），
即f（x）=|2^-x-2|，x∈[-2，0]，
由g（x）=f（x）-|（$\frac{1}{2}$）^x-$\frac{1}{2}$|=0，得f（x）=|（$\frac{1}{2}$）^x-$\frac{1}{2}$|，
设h（x）=|（$\frac{1}{2}$）^x-$\frac{1}{2}$|，
作出函数f（x）和h（x）的图象如图：
当x≤0时，两个函数在[-2016，0]内有1个交点，
在[0，4]内两个函数有3个交点，
当x≥4时，两个函数在每个周期内都有4个交点，此时在[4，2016]内有503×4=2012个交点，
则在[-2016，2016]上解的个数为2012+1+3=2016，
即函数g（x）的零点个数是2016，
故选：B．

点评 本题主要考查函数与方程的应用，根据条件求出一个周期的图象，利用数形结合是解决本题的关键．综合性较强，难度较大．