
设椭圆 +
+ =1(a>b>0)的左,右焦点分别为F1,F2,点P(a,b)满足|PF2|=|F1F2|.
=1(a>b>0)的左,右焦点分别为F1,F2,点P(a,b)满足|PF2|=|F1F2|.
(1)求椭圆的离心率e;
(2)设直线PF2与椭圆相交于A,B两点.若直线PF2与圆(x+1)2+(y- )2=16相交于M,N两点,且|MN|=
)2=16相交于M,N两点,且|MN|=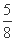 |AB|,求椭圆的方程.
|AB|,求椭圆的方程.
解:(1)设F1(-c,0),F2(c,0)(c>0),
因为|PF2|=|F1F2|,
所以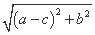 =2c,
=2c,
整理得2( )2+
)2+ -1=0,
-1=0,
得 =-1(舍去),或
=-1(舍去),或 =
= ,
,
所以e= .
.
(2)由(1)知a=2c,b= c,
c,
可得椭圆方程为3x2+4y2=12c2,
直线PF2的方程为y= (x-c).
(x-c).
A、B两点的坐标满足方程组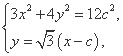
消去y并整理,得5x2-8cx=0,
解得x1=0,x2=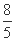 c.
c.
得方程组的解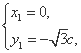
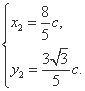
不妨设A(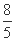 c,
c,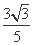 c),B(0,-
c),B(0,- c),
c),
所以|AB|=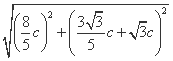 =
=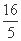 c.
c.
于是|MN|=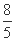 |AB|=2c.
|AB|=2c.
圆心(-1,  )到直线PF2的距离
)到直线PF2的距离
d=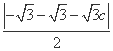 =
=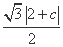 .
.
因为d2+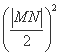 =42,
=42,
所以 (2+c)2+c2=16.
(2+c)2+c2=16.
整理得7c2+12c-52=0,
解得c=- (舍去)或c=2.
(舍去)或c=2.
所以椭圆方程为 +
+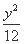 =1.
=1.


科目:高中数学 来源: 题型:
从椭圆 +
+ =1(a>b>0)上一点P向x轴作垂线,垂足恰为左焦点F1,A是椭圆与x轴正半轴的交点,B是椭圆与y轴正半轴的交点,且AB∥OP(O是坐标原点),则该椭圆的离心率是( )
=1(a>b>0)上一点P向x轴作垂线,垂足恰为左焦点F1,A是椭圆与x轴正半轴的交点,B是椭圆与y轴正半轴的交点,且AB∥OP(O是坐标原点),则该椭圆的离心率是( )
(A) (B)
(B) (C)
(C)  (D)
(D)
查看答案和解析>>
科目:高中数学 来源: 题型:
椭圆C:  +
+ =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,a+b=3.
,a+b=3.

(1)求椭圆C的方程;
(2)如图,A,B,D是椭圆C的顶点,P是椭圆C上除顶点外的任意一点,直线DP交x轴于点N,直线AD交BP于点M,设BP的斜率为k,MN的斜率为m.证明2m-k为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
定义:关于x的不等式|x-A|<B的解集叫A的B邻域.
已知a+b-2的a+b邻域为区间(-2,8),其中a、b分别为椭圆 +
+ =1的长半轴长和短半轴长,若此椭圆的一焦点与抛物线y2=4
=1的长半轴长和短半轴长,若此椭圆的一焦点与抛物线y2=4 x的焦点重合,则椭圆的方程为( )
x的焦点重合,则椭圆的方程为( )
(A)  +
+ =1 (B)
=1 (B) 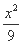 +
+ =1
=1
(C) 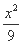 +
+ =1 (D)
=1 (D)  +
+ =1
=1
查看答案和解析>>
科目:高中数学 来源: 题型:
等轴双曲线C的中心在原点,焦点在x轴上,C与抛物线y2=16x的准线交于A、B两点,|AB|=4 ,则C的实轴长为( )
,则C的实轴长为( )
(A) (B)2
(B)2 (C)4 (D)8
(C)4 (D)8
查看答案和解析>>
科目:高中数学 来源: 题型:
某校高一(4)班有男生28人,女生21人,用分层抽样的方法从全体学生中抽取一个调查小组,调查该校学生对2013年元月1日起执行的新交规的知晓情况,已知某男生被抽中的概率为 ,则抽取的女生人数为( )
,则抽取的女生人数为( )
A.1 B.3 C.4 D.7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com