
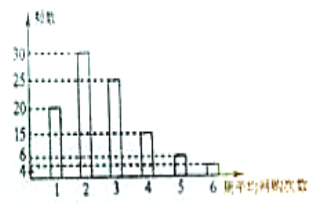
����Ŀ�������ǵ�ǰ���ڹ�����·�ʽ��ij��˾Ϊ�Ľ�Ӫ����ʽ�����������100������ͳ������ƽ�������Ĵ������������õ����µ�Ƶ���ֲ�ֱ��ͼ.��100�������У����䲻����40�����65�˽�������������ƽ������������С��4�ε������Ϊ�����ԣ�����֪������5����������䳬��40��.
��1��������֪������������![]() ���������ܷ��ڷ�����ĸ��ʲ�����0.10��ǰ������Ϊ�����������䲻����40���йأ�
���������ܷ��ڷ�����ĸ��ʲ�����0.10��ǰ������Ϊ�����������䲻����40���йأ�
������ | �������� | �ϼ� | |
���䲻����40�� | |||
���䳬��40�� | |||
�ϼ� |
��2������������������ѡȡ2�������������䳬��40�����������![]() �ķֲ���������.
�ķֲ���������.
����  ��
��
| 0.15 | 0��10 | 0.05 | 0.01 |
| 2.072 | 2.706 | 3.841 | 6.635 |
���𰸡���1�������������2���������.
�����������������
(1)��������������������ɣ����![]()
![]() .���Կ����ڷ�����ĸ��ʲ�����0.10��ǰ������Ϊ�����������䲻����40���йأ�
.���Կ����ڷ�����ĸ��ʲ�����0.10��ǰ������Ϊ�����������䲻����40���йأ�
(2)�÷ֲ���Ϊ�����ηֲ���д���ֲ��пɵ�![]() .
.
���������
��1��������ɵ����������£�
������ | �������� | �ϼ� | |
���䲻����40�� | 20 | 45 | 65 |
���䳬��40�� | 5 | 30 | 35 |
�ϼ� | 25 | 75 | 100 |
���������������䲻����40��û�й�ϵ��
��![]()
![]() .
.
���Կ����ڷ�����ĸ��ʲ�����0.10��ǰ������Ϊ�����������䲻����40���йأ�
��2����Ƶ�ʷֲ�ֱ��ͼ��֪�������Թ���25��������������䳬��40����������![]() ������ȡֵΪ0��1��2��
������ȡֵΪ0��1��2��
![]() ��
�� ![]() ��
�� ![]() ��
��
![]()
![]() �ķֲ���Ϊ
�ķֲ���Ϊ
| 0 | 1 | 2 |
|
|
|
|
![]()
![]() .
.


 ���ɶ��ȫ���ƿؾ�ϵ�д�
���ɶ��ȫ���ƿؾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x���Ķ�����ΪR����f��x����Ϊ��ֵ���������������⣺
�ٺ���g��x��=f��x��+f����x��һ����ż������
����������x��R����f��x��+f��2��x��=0����f��x������2Ϊ���ڵ����ں�����
����f��x�����溯�����Ҷ�������x��R������f��x��+f��2+x��=0����f��x����ͼ��ĶԳ��᷽��Ϊx=2n+1��n��Z����
�ܶ��������x1 �� x2��R����x1��x2 �� ��![]() ��0���������f��x��ΪR�ϵ���������
��0���������f��x��ΪR�ϵ���������
����������ȷ���������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ɣ�����20����ij����Ȼ��������ҩ�ģ����������ȡ20��������������ȷ���ˣ��涨ÿ����ҩ��������С��15��Ϊ����Ʒ.��ͼ��ʾ�ij����ͼ��ʾͳ��20�������е�����Ʒ��������![]() ��ʾÿ��ҩ�ĵ���������ͼ�Т٣�����������Ӧ����������ֱ���____________��
��ʾÿ��ҩ�ĵ���������ͼ�Т٣�����������Ӧ����������ֱ���____________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=xln��x+ ![]() ��a��0��Ϊż������
��a��0��Ϊż������
��1����a��ֵ��
��2����g��x��=ax2+2x+1������[��6��3]�ϵ�ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������ɳ��ذ�����Ϊ�˵������ڵ��������������������׳���������ȡ6�꣬9�꣬12�꣬15�꣬18����������������ݸ�1000�������ݸ������ƽ������������ͼ��ʾ��ɢ��ͼ�ͻع�ֱ��![]() .����ͼ�����ݣ����жԸ���������������ǣ� ��
.����ͼ�����ݣ����жԸ���������������ǣ� ��
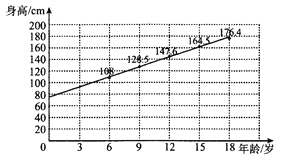
A. ���������ݹ��ƣ��õ�������������������������
B. ����ȡ�����У�5000��������ƽ������ԼΪ![]()
C. ֱ��![]() ��б�ʵ�ֵ���Ƶ���������������ƽ������ÿ�������
��б�ʵ�ֵ���Ƶ���������������ƽ������ÿ�������
D. ����5��������������и�ȡһ�˵��������ݣ�����5�˵�ƽ�������ƽ���������������ĵ�һ����ֱ��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��˫���� ![]() =1��a��0��b��0�������ҽ���ֱ�ΪF1 �� F2�����߷ֱ�Ϊl1 �� l2 �� λ�ڵ�һ���ĵ�P��l1�ϣ���l2��PF1 �� l2��PF2 �� ��˫���ߵ��������ǣ� ��
=1��a��0��b��0�������ҽ���ֱ�ΪF1 �� F2�����߷ֱ�Ϊl1 �� l2 �� λ�ڵ�һ���ĵ�P��l1�ϣ���l2��PF1 �� l2��PF2 �� ��˫���ߵ��������ǣ� ��
A.![]()
B.![]()
C.2
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������A={��x��y��|y=a}������B={��x��y��|y=bx+1��b��0��b��1}��������A��B������ʵ��a��ȡֵ��Χ�ǣ� ��
A.�����ޣ�1��
B.�����ޣ�1]
C.[1��+�ޣ�
D.��1��+�ޣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ABC��A1B1C1�У�D��BC���е㣮 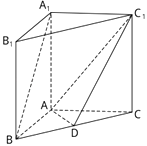
��1����֤��A1B��ƽ��ADC1��
��2����AB��AC��AB=AC=1��AA1=2������ABD��A1B1C1�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���輯��A={x|2a��1��x��a+3}������B={x|x����1��x��5}��
��1����a=��2ʱ����A��B��
��2����AB����ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com