
分析 由切线方程可得g(1)=-8,可得f(1)=g(1)+1,求出g′(1)=-9,求出f(x)的导数,可得f′(1)=g′(1)+2,由点斜式方程即可得到所求方程.
解答 解:曲线y=g(x)在点(1,g(1))处的切线方程为9x+y-1=0,
可得g(1)=-8,g′(1)=-9,
则f(1)=g(1)+1=-8+1=-7.
由f′(x)=g′(x)+2x,
可得f′(1)=g′(1)+2=-9+2=-7,
曲线y=f(x)在点(1,f(1))处的切线方程为y+7=-7(x-1),
即为7x+y=0,
故答案为:7x+y=0.
点评 本题考查导数的运用:求切线的方程,考查导数的几何意义,正确求导和运用点斜式方程是解题的关键,考查运算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,一直角墙角,两边的长度足够长,若P处有一棵树与两墙的距离分别是2m和αm(0<α<10),不考虑树的粗细,现用12m长的篱笆,借助墙角围成一个矩形花圃ABCD,设此矩形花圃的最大面积为u,若将这棵树围在矩形花圃内,则函数u=f(a)(单位:m2)的图象大致是( )
如图,一直角墙角,两边的长度足够长,若P处有一棵树与两墙的距离分别是2m和αm(0<α<10),不考虑树的粗细,现用12m长的篱笆,借助墙角围成一个矩形花圃ABCD,设此矩形花圃的最大面积为u,若将这棵树围在矩形花圃内,则函数u=f(a)(单位:m2)的图象大致是( )| A. |  | B. |  | ||
| C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
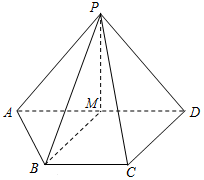 如图,在四棱锥P-ABCD中,M为AD的中点.
如图,在四棱锥P-ABCD中,M为AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com