
分析 (1)根据f(x)=$\overrightarrow{m}$•$\overrightarrow{n}$.向量的运算,求出f(x)的解析式,即可求函数f(x)的最小正周期和单调递增区间.
(2)利用正弦函数化简(2a-b)cosC=ccosB,根据$f(A)=\frac{3}{2}$,求出角A,正弦定理求出c.
解答 解:(1)$\overrightarrow{m}$=($\sqrt{3}$sin$\frac{x}{3}$,cos$\frac{x}{3})$,$\overrightarrow{n}$=(cos$\frac{x}{3}$,cos$\frac{x}{3}$),
∵f(x)=$\overrightarrow{m}•\overrightarrow{n}$=$\sqrt{3}sin\frac{x}{3}cos\frac{x}{3}+{cos^2}\frac{x}{3}$=$\frac{{\sqrt{3}}}{2}sin\frac{2x}{3}+\frac{1}{2}(cos\frac{2x}{3}+1)$=$sin(\frac{2x}{3}+\frac{π}{6})+\frac{1}{2}$,
∴f(x)的最小正周期T=$\frac{2π}{\frac{2}{3}}$=3π,
令$-\frac{π}{2}+2kπ≤\frac{2x}{3}+\frac{π}{6}≤\frac{π}{2}+2kπ$,k∈Z,
得:$-π+3kπ≤x≤\frac{π}{2}+3kπ$,
∴f(x)的单调递增区间为$[-π+3kπ,\frac{π}{2}+3kπ]$(k∈Z);
(2)∵(2a-b)cosC=ccosB,
由正弦定理,得:2sinAcosC=sinBcosC+cosBsinC=sinA,
∵0<A<π,0<C<π.
∴sinA>0,
∴$cosC=\frac{1}{2}$,
∴$C=\frac{π}{3}$,
又∵$f(A)=\frac{3}{2}$,即$f(A)=sin(\frac{2A}{3}+\frac{π}{6})+\frac{1}{2}=\frac{3}{2}$,
∴$sin(\frac{2A}{3}+\frac{π}{6})=1$,
∴$\frac{2A}{3}+\frac{π}{6}=\frac{π}{2}+2kπ$,k∈Z,
∴$A=\frac{π}{2}$,
正弦定理,可得:$c=asinC=2sin\frac{π}{3}=\sqrt{3}$.
点评 本题考查了三角函数的化解和计算能力,性质的运用和正弦定理的计算.属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | 1 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{4}$ | B. | $\frac{3}{4}$ | C. | $-\frac{4}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2) | B. | [-2,+∞) | C. | (1,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
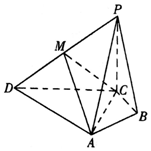 在四棱锥P-ABCD中,PC⊥底面ABCD,M是PD的中点,AC⊥AD,BA⊥BC,PC=AC=2BC,∠ACD=∠ACB.
在四棱锥P-ABCD中,PC⊥底面ABCD,M是PD的中点,AC⊥AD,BA⊥BC,PC=AC=2BC,∠ACD=∠ACB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com