
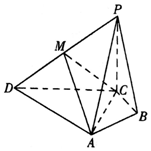
 在四棱锥P-ABCD中,PC⊥底面ABCD,M是PD的中点,AC⊥AD,BA⊥BC,PC=AC=2BC,∠ACD=∠ACB.
在四棱锥P-ABCD中,PC⊥底面ABCD,M是PD的中点,AC⊥AD,BA⊥BC,PC=AC=2BC,∠ACD=∠ACB.分析 (1)取PA的中点N,连接MN,NC,由三角形中位线定理可得MN∥AD,由PC⊥底面ABCD,得PC⊥AD,结合AC⊥AD,可得AD⊥平面PAC,进一步得到MN⊥PA,再由等腰三角形的性质可知CN⊥PA,由线面垂直的判定得到PA⊥平面MNC,则有PA⊥CM;
(2)设PC=AC=1,解三角形可得CD=2.以B为坐标原点,以BA、CB所在直线分别为x、y轴,以过B点和PC平行的直线为z轴距离如图所示坐标系.求得A,C,D,P的坐标,进一步求出平面PAC与平面ACM的一个法向量,利用两法向量所成角的余弦值可得二面角M-AC-P的余弦值.
解答 (1)证明:取PA的中点N,连接MN,NC,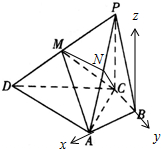
∵MN为△PAD的中位线,∴MN∥AD,
∵PC⊥底面ABCD,∴PC⊥AD,
又∵AC⊥AD,PC∩AD=C,∴AD⊥平面PAC,
∴AD⊥PA,则MN⊥PA,
∵PC=AC,N为PA的中点,∴CN⊥PA,
∵MN∩NC=N,∴PA⊥平面MNC,
又∵CM?平面MNC,∴PA⊥CM;
(2)解:设PC=AC=1,则BC=$\frac{1}{2}$,
∵BA⊥BC,∴cos$∠ACB=\frac{1}{2}$,
∴∠ACD=∠ACB=60°,
又∵AC⊥CD,∴CD=2.
以B为坐标原点,以BA、CB所在直线分别为x、y轴,以过B点和PC平行的直线为z轴距离如图所示坐标系.
则A($\frac{\sqrt{3}}{2}$,0,0),C(0,-$\frac{1}{2}$,0),D($\sqrt{3}$,-$\frac{3}{2}$,0),P(0,-$\frac{1}{2}$,1),
∴M($\frac{\sqrt{3}}{2}$,-1,$\frac{1}{2}$).
$\overrightarrow{CA}=(\frac{\sqrt{3}}{2},\frac{1}{2},0),\overrightarrow{CM}=(\frac{\sqrt{3}}{2},-\frac{1}{2},\frac{1}{2})$,$\overrightarrow{DA}=(-\frac{\sqrt{3}}{2},\frac{3}{2},0)$.
∵DA⊥平面PAC,
∴$\overrightarrow{DA}=(-\frac{\sqrt{3}}{2},\frac{3}{2},0)$是平面PAC的一个法向量.
设$\overrightarrow{n}=(x,y,z)$是平面ACM的一个法向量,
则$\left\{\begin{array}{l}{\overrightarrow{CA}•\overrightarrow{n}=0}\\{\overrightarrow{CM}•\overrightarrow{n}=0}\end{array}\right.$,即$\left\{\begin{array}{l}{\frac{\sqrt{3}}{2}x+\frac{1}{2}y=0}\\{\frac{\sqrt{3}}{2}x-\frac{1}{2}y+\frac{z}{2}=0}\end{array}\right.$,令x=1,得$\overrightarrow{n}=(1,-\sqrt{3},-2\sqrt{3})$.
∴|cos<$\overrightarrow{DA},\overrightarrow{n}$>|=|$\frac{\overrightarrow{DA}•\overrightarrow{n}}{|\overrightarrow{DA}|•|\overrightarrow{n}|}$|=|$\frac{-\frac{\sqrt{3}}{2}-\frac{3\sqrt{3}}{2}}{\sqrt{3}×4}$|=$\frac{1}{2}$.
由图可知,二面角M-AC-P为锐角,
∴二面角M-AC-P的余弦值为$\frac{1}{2}$.
点评 本题考查线面垂直的判定和性质,考查空间想象能力和思维能力,训练了利用空间向量求二面角的平面角,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
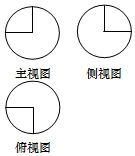 如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径,若该几何体的体积是$\frac{28π}{3}$,则三视图中圆的半径为( )
如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径,若该几何体的体积是$\frac{28π}{3}$,则三视图中圆的半径为( )| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x±y=0 | B. | x±$\frac{\sqrt{3}}{3}$y=0 | C. | x±$\frac{\sqrt{2}}{2}$y=0 | D. | x±2y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,3) | B. | (-∞,2]∪[3,+∞) | C. | (0,2]∪[3,+∞) | D. | [3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
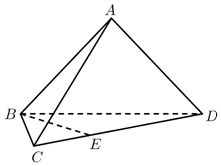 如图,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,∠CBD=60°,BD=2BC=4,点E在CD上,DE=2EC.
如图,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,∠CBD=60°,BD=2BC=4,点E在CD上,DE=2EC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
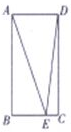 在如图所示的矩形ABCD中,AB=4,AD=2,E为线段BC上的点,则$\overrightarrow{AE}•\overrightarrow{DE}$的最小值为( )
在如图所示的矩形ABCD中,AB=4,AD=2,E为线段BC上的点,则$\overrightarrow{AE}•\overrightarrow{DE}$的最小值为( )| A. | 12 | B. | 15 | C. | 17 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com