
分析 若函数f(x)=$\left\{\begin{array}{l}xlnx-a{x^2},x≥1\\{a^x},x<1\end{array}$是减函数,故每一段上函数均为减函数,且a>f(1),利用导数法,可得a的取值范围.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}xlnx-a{x^2},x≥1\\{a^x},x<1\end{array}$是减函数,
∴0<a<1,
当x≥1时,f′(x)=1+lnx-2ax≤0,2a≥$\frac{1+lnx}{x}$,
设h(x)=$\frac{1+lnx}{x}$,则h′(x)=$\frac{-lnx}{x^2}$=0,解得:x=1,
故h(x)在x=1处取得最大值1,
故2a≥1,即a≥$\frac{1}{2}$,
又a>f(1)=-a,
故a∈[$\frac{1}{2}$,1).
故答案为:[$\frac{1}{2}$,1)
点评 本题考查的知识点是分段函数的应用,正确理解分段函数单调性的意义,是解答的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{14}{9}$ | C. | $\frac{9}{14}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
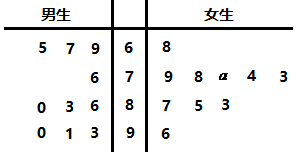 某中学为了普及法律知识,举行了一次法律知识竞赛活动.下面的茎叶图记录了男生、女生各10名学生在该次竞赛活动中的成绩(单位:分).
某中学为了普及法律知识,举行了一次法律知识竞赛活动.下面的茎叶图记录了男生、女生各10名学生在该次竞赛活动中的成绩(单位:分).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{5}$ | B. | $\frac{1}{5}$ | C. | $-\frac{3}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com