
【题目】全世界越来越关注环境保护问题,某省一监测站点于2016年8月某日起连续![]() 天监测空气质量指数
天监测空气质量指数![]() ,数据统计如下:
,数据统计如下:

(Ⅰ)根据所给统计表和频率分布直方图中的信息求出![]() 、
、![]() 的值,并完成频率分布直方图;
的值,并完成频率分布直方图;
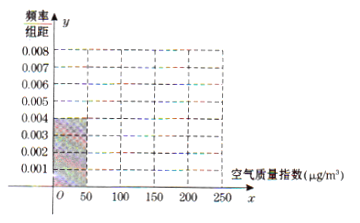
(Ⅱ)在空气质量指数分别为![]() 和
和![]() 的监测数据中,用分层抽样的方法抽取5天,从中任意选取2天,求事件
的监测数据中,用分层抽样的方法抽取5天,从中任意选取2天,求事件![]() “两天空气都为良”发生的概率.
“两天空气都为良”发生的概率.
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)由所给统计表和频率分布直方图中的信息能求出![]() 、
、![]() 的值,并完成频率分布直方图;(Ⅱ)在空气质量指数为
的值,并完成频率分布直方图;(Ⅱ)在空气质量指数为![]() 和
和![]() 的监测天数中分别抽取4天和1天,在所抽取的5天中,将空气质量指数为
的监测天数中分别抽取4天和1天,在所抽取的5天中,将空气质量指数为![]() 的4天分别记为
的4天分别记为![]() ,
, ![]() ,
, ![]() ,
, ![]() ;将空气污染指数为
;将空气污染指数为![]() 的1天记为
的1天记为![]() ,由此利用列举法能求出事件A“两天空气都为良”发生的概率.
,由此利用列举法能求出事件A“两天空气都为良”发生的概率.
试题解析:(Ⅰ) ![]() ,
, ![]() .
.
![]() ,
, ![]() .
.
![]() ,
, ![]() ,
, ![]() ,
,
![]()
(Ⅱ)在空气质量指数为51-100和151-200的监测天数中分别抽取4天和1天,在所抽取的5天中,将空气质量指数为51-100的4天分别记为![]() ,
, ![]() ,
, ![]() ,
, ![]() ;将空气污染指数为151-200的1天记为
;将空气污染指数为151-200的1天记为![]() ,
,
从中任取2天的基本事件分别为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 共10种,
共10种,
其中事件![]() “两天空气都为良”包含的基本事件为
“两天空气都为良”包含的基本事件为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 共6种,
共6种,
所以事件![]() “两天都为良”发生的概率是
“两天都为良”发生的概率是![]() .
.


科目:高中数学 来源: 题型:
【题目】如图所示,M、N、P分别是正方体ABCD-A1B1C1D1的棱AB、BC、DD1上的点.
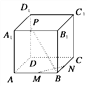
(1)若![]() ,求证:无论点P在DD1上如何移动,总有BP⊥MN;
,求证:无论点P在DD1上如何移动,总有BP⊥MN;
(2)棱DD1上是否存在这样的点P,使得平面APC1⊥平面ACC1?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的奇函数.
上的奇函数.
(1)求![]() 的解析式;
的解析式;
(2)证明:函数![]() 在定义域上是增函数;
在定义域上是增函数;
(3)设![]() 是否存在正实数
是否存在正实数![]() 使得函数
使得函数![]() 在
在![]() 内的最小值为
内的最小值为![]() ?若存在,求出
?若存在,求出![]() 的值;若存在,请说明理由.
的值;若存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
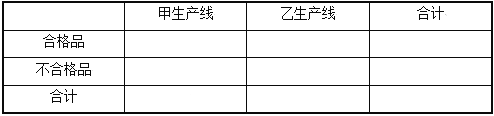
【题目】某企业生产的某种产品被检测出其中一项质量指标存在问题.该企业为了检查生产该产品的甲,乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.表1是甲流水线样本的频数分布表,图1是乙流水线样本的频率分布直方图.
内,则为合格品,否则为不合格品.表1是甲流水线样本的频数分布表,图1是乙流水线样本的频率分布直方图.
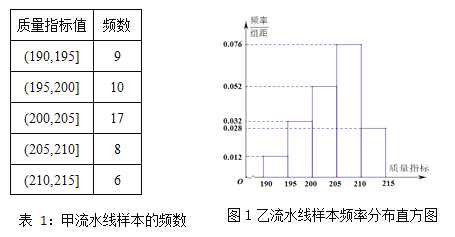
(1)根据图,1估计乙流水线生产产品该质量指标值的中位数;
(2)若将频率视为概率,某个月内甲,乙两条流水线均生产了5000件产品,则甲,乙两条流水线分别生产出不合格品约多少件?
(3)根据已知条件完成下面![]() 列联表,并回答是否有85%的把握认为“该企业生产的这种产品的质量指标值与甲,乙两条流水线的选择有关”?
列联表,并回答是否有85%的把握认为“该企业生产的这种产品的质量指标值与甲,乙两条流水线的选择有关”?
附: ![]() (其中
(其中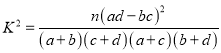 为样本容量)
为样本容量)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某项考试按科目A、科目B依次进行,只有当科目A成绩合格时,才可继续参加科目B的考试.已知每个科目只允许有一次补考机会,两个科目成绩均合格方可获得证书.现某人参加这项考试,科目A每次考试成绩合格的概率均为![]() ,科目B每次考试成绩合格的概率均为
,科目B每次考试成绩合格的概率均为![]() .假设各次考试成绩合格与否均互不影响.
.假设各次考试成绩合格与否均互不影响.
(1)求他不需要补考就可获得证书的概率;
(2)在这项考试过程中,假设他不放弃所有的考试机会,记他参加考试的次数为![]() ,求
,求![]() 的分布列及数学期望E
的分布列及数学期望E![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产的乒乓球被指定为乒乓球比赛专用球.日前有关部门对某批产品进行了抽样检测,检测结果如下表所示:
抽取球数n | 50 | 100 | 200 | 500 | 1 000 | 2 000 |
优等品数m | 45 | 92 | 194 | 470 | 954 | 1 902 |
优等品频率 |
(1)计算表中乒乓球为优等品的频率.
(2)从这批乒乓球产品中任取一个,检测出为优等品的概率是多少?(结果保留到小数点后三位)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点, ![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求出圆![]() 的直角坐标方程;
的直角坐标方程;
(2)已知圆![]() 与
与![]() 轴相交于
轴相交于![]() ,
, ![]() 两点,直线
两点,直线![]() :
: ![]() 关于点
关于点![]() 对称的直线为
对称的直线为![]() .若直线
.若直线![]() 上存在点
上存在点![]() 使得
使得![]() ,求实数
,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com