
【题目】已知![]() ,函数
,函数![]() .
.
(Ⅰ)求![]() 在区间
在区间![]() 上的最小值;
上的最小值;
(Ⅱ)设![]() ,当
,当![]() 时,
时, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ) ![]() ;(Ⅱ)
;(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ) 利用![]() 得
得![]() ,判断函数的单调性,通过(i)当
,判断函数的单调性,通过(i)当![]() 时;(ii)当
时;(ii)当![]() 时,(iii)当
时,(iii)当![]() 时,分别求解函数的最值;(Ⅱ)
时,分别求解函数的最值;(Ⅱ) ![]() ,则
,则![]() ,通过①当
,通过①当![]() 时,②当
时,②当![]() 时,i当
时,i当![]() 时,ii当
时,ii当![]() 时,利用函数的导数结合函数的单调性求解函数的最值,推出实数
时,利用函数的导数结合函数的单调性求解函数的最值,推出实数![]() 的取值范围.
的取值范围.
试题解析:(Ⅰ) ![]() ,由
,由![]() ,得
,得![]() ,
,
当![]() 时,
时, ![]() 为增函数;
为增函数;
当![]() 时,
时, ![]() 为减函数.
为减函数.
(i)当![]() 时,
时, ![]() 在区间
在区间![]() 上为减函数,
上为减函数, ![]() ;
;
(ii)当![]() 时,
时, ![]() 在区间
在区间![]() 上为增函数,
上为增函数, ![]() ;
;
(iii)当![]() 时,
时, ![]() ,
,
若![]() 时,
时, ![]() ; 若
; 若![]() 时,
时, ![]() .
.
综上,当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
(Ⅱ) ![]() ,则
,则![]() .
.
①当![]() 时,
时, ![]() 在
在![]() 上单调递增,则
上单调递增,则![]() ,
,
∵![]() ,∴存在
,∴存在![]() ,使得
,使得![]() ,于是
,于是![]() 在区间
在区间![]() 上单调递减,当
上单调递减,当![]() 时,
时, ![]() 与
与![]() 恒成立相矛盾,不符合题意.
恒成立相矛盾,不符合题意.
②当![]() 时,
时, ![]() ),则
),则![]() ,即
,即![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,即
,即![]() ,∴
,∴![]() .
.
(i)当![]() 时,
时, ![]() ,于是
,于是![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() 恒成立,符合题意.
恒成立,符合题意.
(ii)当![]() 时,
时, ![]() 在
在![]() 上单调递增,
上单调递增,
则![]() ,即
,即![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,
,
∵![]() ,∴存在
,∴存在![]() ,使得
,使得![]() ,于是
,于是![]() 在区间
在区间![]() 上单调递减,
上单调递减,
当![]() 时,
时, ![]() 与
与![]() 恒成立相矛盾,不符合题意.
恒成立相矛盾,不符合题意.
综上,实数![]() 的取值范围是
的取值范围是![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数,
为常数, ![]() 是自然对数的底数),曲线
是自然对数的底数),曲线![]() 在点
在点![]() 处的切线方程是
处的切线方程是![]() .
.
(1)求![]() 的值;(2)求
的值;(2)求![]() 的单调区间;
的单调区间;
(3)设![]() (其中
(其中![]() 为
为![]() 的导函数)。证明:对任意
的导函数)。证明:对任意![]() ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分) 设函数![]()
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)令![]() <
<![]() ≤
≤![]() ,其图像上任意一点P
,其图像上任意一点P![]() 处切线的斜率
处切线的斜率![]() ≤
≤![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,方程
时,方程![]() 在区间
在区间![]() 内有唯一实数解,求实数
内有唯一实数解,求实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“珠算之父”程大为是我国明代伟大数学家,他的应用数学巨著《算法统综》的问世,标志着我国的算法由筹算到珠算转变的完成,程大位在《算法统综》中常以诗歌的形式呈现数学问题,其中有一首“竹筒容米”问题:“家有九节竹一茎,为因盛米不均平,下头三节三升九,上稍四节储三升,唯有中间两节竹,要将米数次第盛,若有先生能算法,也教算得到天明”(【注】三升九:3.9升,次第盛;盛米容积依次相差同一数量.)用你所学的数学知识求得中间两节的容积为( )
A. ![]() 升 B.
升 B. ![]() 升 C.
升 C. ![]() 升 D.
升 D. ![]() 升
升
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若f(1)=0,求函数f(x)的最大值;
(Ⅱ)令![]() ,讨论函数g(x)的单调区间;
,讨论函数g(x)的单调区间;
(Ⅲ)若a=2,正实数x1,x2满足![]() 证明
证明![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(数学文卷·2017届北京市朝阳区高三上学期期中考试第14题) 《九章算术》是我国古代一部重要的数学著作.书中有如下问题:“今有良马与驽马发长安,至齐。齐去长安三千里,良马初日行一百九十三里,日增一十三里;驽马初日行九十七里,日减半里.良马先至齐,复还迎驽马.问几何日相逢.”其意为:“现在有良马和驽马同时从长安出发到齐去.已知长安和齐的距离是3000里,良马第一天行193里,之后每天比前一天多行13里;驽马第一天行97里,之后每天比前一天少行0.5里.良马到齐后,返回去迎驽马.多少天后两马相遇.”利用我们所学的知识,可知离开长安后的第______天,两马相逢.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】全世界越来越关注环境保护问题,某省一监测站点于2016年8月某日起连续![]() 天监测空气质量指数
天监测空气质量指数![]() ,数据统计如下:
,数据统计如下:

(Ⅰ)根据所给统计表和频率分布直方图中的信息求出![]() 、
、![]() 的值,并完成频率分布直方图;
的值,并完成频率分布直方图;
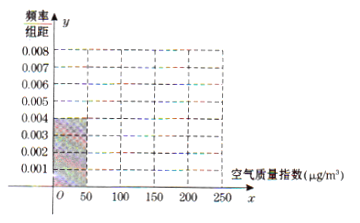
(Ⅱ)在空气质量指数分别为![]() 和
和![]() 的监测数据中,用分层抽样的方法抽取5天,从中任意选取2天,求事件
的监测数据中,用分层抽样的方法抽取5天,从中任意选取2天,求事件![]() “两天空气都为良”发生的概率.
“两天空气都为良”发生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com