
【题目】已知函数![]() (
(![]() 为常数,
为常数, ![]() 是自然对数的底数),曲线
是自然对数的底数),曲线![]() 在点
在点![]() 处的切线方程是
处的切线方程是![]() .
.
(1)求![]() 的值;(2)求
的值;(2)求![]() 的单调区间;
的单调区间;
(3)设![]() (其中
(其中![]() 为
为![]() 的导函数)。证明:对任意
的导函数)。证明:对任意![]() ,
, ![]()
科目:高中数学 来源: 题型:
【题目】如图,已知平面![]() 平面
平面![]() ,四边形
,四边形![]() 是正方形,四边形
是正方形,四边形![]() 是菱形,且
是菱形,且![]() ,
,![]() ,点
,点![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 上的动点.
上的动点.
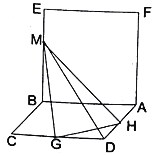
(1)求证:![]()
![]() ;
;
(2)求三棱锥![]() 的体积的最大值.
的体积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设人的某一特征(如眼睛的大小)是由他的一对基因所决定,以d表示显性基因,r表示隐性基因,则具有dd基因的人为纯显性,具有rr基因的人为纯隐性,具有rd基因的人为混合性,纯显性与混合性的人都显露显性基因决定的某一特征,孩子从父母身上各得到一个基因,假定父母都是混合性,问:
(1)1个孩子显露显性特征的概率是多少?
(2)“该父母生的2个孩子中至少有1个显露显性特征”,这种说法正确吗?
查看答案和解析>>
科目:高中数学 来源: 题型:
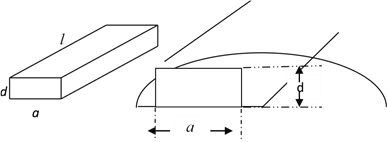
【题目】一根水平放置的长方体形枕木的安全负荷与它的宽度![]() 成正比,与它的厚度
成正比,与它的厚度![]() 的平方成正比,与它的长度
的平方成正比,与它的长度![]() 的平方成反比.
的平方成反比.
(Ⅰ)将此枕木翻转90°(即宽度变为厚度),枕木的安全负荷会如何变化?为什么?(设翻转前后枕木的安全负荷分别为![]() 且翻转前后的比例系数相同都为
且翻转前后的比例系数相同都为![]() )
)
(Ⅱ)现有一根横断面为半圆(已知半圆的半径为![]() )的木材,用它来截取成长方体形的枕木,其长度为10,问截取枕木的厚度为
)的木材,用它来截取成长方体形的枕木,其长度为10,问截取枕木的厚度为![]() 多少时,可使安全负荷
多少时,可使安全负荷![]() 最大?
最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() ,过
,过![]() 、
、![]() 、
、![]() 三点的圆
三点的圆![]() 的圆心坐标为
的圆心坐标为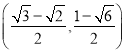 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线![]() (
(![]() 为常数,
为常数, ![]() )与椭圆
)与椭圆![]() 交于不同的两点
交于不同的两点![]() 和
和![]() .
.
(ⅰ)当直线![]() 过
过![]() ,且
,且![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(ⅱ)当坐标原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,且
,且![]() 面积为
面积为![]() 时,求直线
时,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在高中学习过程中,同学们经常这样说:“如果物理成绩好,那么学习数学就没什么问题.”某班针对“高中生物理学习对数学学习的影响”进行研究,得到了学生的物理成绩与数学成绩具有线性相关关系的结论.现从该班随机抽取5名学生在一次考试中的物理和数学成绩,如下表:
编号 成绩 | 1 | 2 | 3 | 4 | 5 |
物理( | 90 | 85 | 74 | 68 | 63 |
数学( | 130 | 125 | 110 | 95 | 90 |
(1)求数学成绩![]() 关于物理成绩
关于物理成绩![]() 的线性回归方程
的线性回归方程![]() (
(![]() 精确到
精确到![]() ),若某位学生的物理成绩为80分,预测他的数学成绩;
),若某位学生的物理成绩为80分,预测他的数学成绩;
(2)要从抽取的五位学生中随机选出三位参加一项知识竞赛,以![]() 表示选中的学生的数学成绩高于100分的人数,求随机变量
表示选中的学生的数学成绩高于100分的人数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
(参数公式: 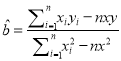 ,
, ![]() .)
.)
参考数据: ![]() ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,M、N、P分别是正方体ABCD-A1B1C1D1的棱AB、BC、DD1上的点.
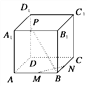
(1)若![]() ,求证:无论点P在DD1上如何移动,总有BP⊥MN;
,求证:无论点P在DD1上如何移动,总有BP⊥MN;
(2)棱DD1上是否存在这样的点P,使得平面APC1⊥平面ACC1?证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com