
报废年限 车型 | 1年 | 2年 | 3年 | 4年 | 总计 |
| A | 20 | 35 | 35 | 10 | 100 |
| B | 10 | 30 | 40 | 20 | 100 |
分析 (Ⅰ)求出回归系数,可得回归方程,即可得出结论;
(Ⅱ)分别计算相应的数学期望,即可得出结论.
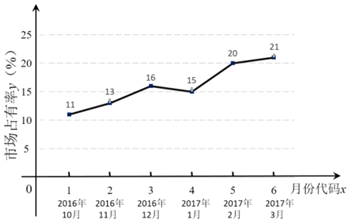
解答 解:(Ⅰ)由题意,$\overline{x}$=3.5,$\overline{y}$=16,$\widehat{b}$=$\frac{35}{17.5}$=2,$\widehat{a}$=$\overline{y}$-$\widehat{b}$•$\overline{x}$=16-2×3.5=9,
∴$\widehat{y}$=2x+9,
x=7时,$\widehat{y}$=2×7+9=23,即预测M公司2017年4月份(即x=7时)的市场占有率为23%;
(Ⅱ)由频率估计概率,每辆A款车可使用1年,2年,3年、4年的概率分别为0.2,0.35,0.35,0.1,
∴每辆A款车的利润数学期望为(500-1000)×0.2+(1000-1000)×0.35+(1500-1000)×0.35+(2000-1000)×0.1=175元;
每辆B款车可使用1年,2年,3年、4年的概率分别为0.1,0.3,0.4,0.2,
∴每辆B款车的利润数学期望为(500-1200)×0.1+(1000-1200)×0.3+(1500-1200)×0.4+(2000-1200)×0.2=150元;
∵175>150,
∴应该采购A款车.
点评 本题考查数学知识在实际生活中的应用,考查学生的阅读能力,对数据的处理能力,属于中档题.


科目:高中数学 来源: 题型:选择题
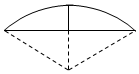 《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积=$\frac{1}{2}×$(弦×矢+矢2),弧田(如图)由圆弧和其所对弦围城,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角$\frac{2π}{3}$,半径为6米的弧田,按照上述经验公式计算所得弧田面积约是($\sqrt{3}≈1.73$)( )
《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积=$\frac{1}{2}×$(弦×矢+矢2),弧田(如图)由圆弧和其所对弦围城,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角$\frac{2π}{3}$,半径为6米的弧田,按照上述经验公式计算所得弧田面积约是($\sqrt{3}≈1.73$)( )| A. | 16平方米 | B. | 18平方米 | C. | 20平方米 | D. | 25平方米 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了解某地高中生的身高情况,研究小组在该地高中生中随机抽出30名高中生的身高统计成如图所示的茎叶图(单位:cm).
为了解某地高中生的身高情况,研究小组在该地高中生中随机抽出30名高中生的身高统计成如图所示的茎叶图(单位:cm).查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com