
分析 (1)由c=2$\sqrt{2}$,a-c=3-2$\sqrt{2}$.a=3,b2=a2-c2=1即可求得椭圆方程;
(2)方法一:设直线方程为y=-2x+t,代入椭圆方程,利用韦达定理及中点坐标公式,消去t,即可求得轨迹方程,代入椭圆方程,即可求得x的取值范围;方法二:利用设而不求法,将E和F坐标代入椭圆方程,作差,根据中点坐标公式,即可求得即可求得轨迹方程,代入椭圆方程,即可求得x的取值范围;
(3)设直线方程,代入椭圆方程,利用韦达定理,弦长公式,根据函数的单调性即可求得△PQO的面积的最大值.
解答 解:(1)椭圆的焦点为${F_1}(-2\sqrt{2},0),{F_2}(2\sqrt{2},0)$,c=2$\sqrt{2}$,
由a-c=3-2$\sqrt{2}$.a=3,则b2=a2-c2=1
故曲线C的方程为$\frac{x^2}{9}+{y^2}=1$.
(2)方法1:设A(x1,y1),B(x2,y2),N(x,y),设直线方程为y=-2x+t,
$\left\{\begin{array}{l}{y=-2x+t}\\{\frac{{x}^{2}}{9}+{y}^{2}=1}\end{array}\right.$,$\frac{37}{9}{x}^{2}$-4tx+t2-1=0,$2x={x_1}+{x_2}=\frac{36}{37}t\;,\;2y={y_1}+{y_2}=-2({x_1}+{x_2})+2t=\frac{2}{37}t$,
∴x-18y=0,
$\left\{\begin{array}{l}{x-18y=0}\\{\frac{{x}^{2}}{9}+{y}^{2}=1}\end{array}\right.$,则x2=±$\frac{18\sqrt{37}}{37}$,则-$\frac{18\sqrt{37}}{37}$<x<$\frac{18\sqrt{37}}{37}$,
∴线段EF的中点N的轨迹方程是:x-18y=0,-$\frac{18\sqrt{37}}{37}$<x<$\frac{18\sqrt{37}}{37}$,
方法2:设A(x1,y1),B(x2,y2),N(x,y),则x1+x2=2x,y1+y2=2y.
∵A、B在曲线C上,
∴$x_1^2+9y_1^2=9$,$x_2^2+9y_2^2=9$.
将以上两式相减得:(x1-x2)(x1+x2)+9(y1-y2)(y2+y2)=0,即$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=-$\frac{{x}_{1}+{x}_{2}}{9({y}_{1}+{y}_{2})}$,
则-2=-$\frac{x}{9y}$,
∴线段EF的中点N的轨迹方程:x-18y=0,-$\frac{18\sqrt{37}}{37}$<x<$\frac{18\sqrt{37}}{37}$;
(3)设直线PQ的方程是:my=x+2$\sqrt{2}$,x=my-2$\sqrt{2}$,
代入$\frac{x^2}{9}+{y^2}=1$得$({m^2}+9){y^2}-4\sqrt{2}my-1=0$.
设P(x1,y1),Q(x2,y2),${y_1}+{y_2}=\frac{{4\sqrt{2}m}}{{{m^2}+9}}$,${y_1}•{y_2}=\frac{-1}{{{m^2}+9}}$,
则$|{y_1}-{y_2}|\;=6\sqrt{\frac{{{m^2}+1}}{{{{({m^2}+9)}^2}}}}$,
令t=m2+9≥9,$|{y_1}-{y_2}|\;=6\sqrt{\frac{t-8}{t^2}}=6\sqrt{-\frac{8}{t^2}+\frac{1}{t}}=6\sqrt{-8{{(\frac{1}{t}-\frac{1}{16})}^2}+\frac{8}{{{{16}^2}}}}$,
当t=16,即$m=±\sqrt{7}$时,
∴${({S_{△OPQ}})_{max}}=\frac{1}{2}|OF|•|{y_1}-{y_2}|\;=\frac{3}{2}$,
△PQO的面积的最大值为$\frac{3}{2}$.
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查韦达定理,弦长公式,轨迹方程的求法,考查函数单调性与椭圆的综合应用,考查计算能力,属于中档题.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c>b>a | B. | a>b>c | C. | a>c>b | D. | b>a>c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
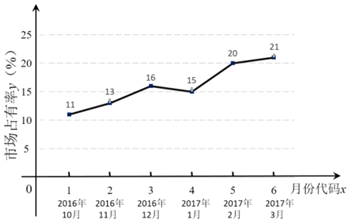
报废年限 车型 | 1年 | 2年 | 3年 | 4年 | 总计 |
| A | 20 | 35 | 35 | 10 | 100 |
| B | 10 | 30 | 40 | 20 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
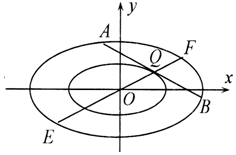 在直角坐标系xOy中,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,左、右焦点分别是F1,F2,P为椭圆C1上任意一点,|PF1|+|PF2|的最大值为4.
在直角坐标系xOy中,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,左、右焦点分别是F1,F2,P为椭圆C1上任意一点,|PF1|+|PF2|的最大值为4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com