
分析 (1)先求出$\overrightarrow{a}$•$\overrightarrow{b}$=-3,再根据向量的数量积计算即可,
(2)先平方,再根据向量的数量积运算即可.
解答 解:(1)∵|$\overrightarrow{a}$|=3,|$\overrightarrow{b}$|=2,且$\overrightarrow a,\overrightarrow b$的夹角为120°,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|•cos120°=3×2×(-$\frac{1}{2}$)=-3,
∴$({2\overrightarrow a+\overrightarrow b})•({\overrightarrow a-2\overrightarrow b})$=2|$\overrightarrow{a}$|2-3$\overrightarrow{a}$$•\overrightarrow{b}$-2|$\overrightarrow{b}$|2=2×9-3×(-3)-2×4=19
(2)|2$\overrightarrow{a}$+$\overrightarrow{b}$|2=4|$\overrightarrow{a}$|2+4$\overrightarrow{a}$$•\overrightarrow{b}$+|$\overrightarrow{b}$|2=36-12+4=28,
∴|2$\overrightarrow{a}$+$\overrightarrow{b}$|2=2$\sqrt{7}$.
点评 本题考查向量的数量积的运算,向量的夹角公式,向量的模,考查计算能力,属于基础题


科目:高中数学 来源: 题型:选择题
| A. | y=±$\frac{1}{2}$x | B. | y=±$\sqrt{3}$x | C. | y=±2x | D. | y=±$\frac{{\sqrt{3}}}{3}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
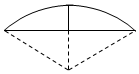 《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积=$\frac{1}{2}×$(弦×矢+矢2),弧田(如图)由圆弧和其所对弦围城,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角$\frac{2π}{3}$,半径为6米的弧田,按照上述经验公式计算所得弧田面积约是($\sqrt{3}≈1.73$)( )
《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积=$\frac{1}{2}×$(弦×矢+矢2),弧田(如图)由圆弧和其所对弦围城,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角$\frac{2π}{3}$,半径为6米的弧田,按照上述经验公式计算所得弧田面积约是($\sqrt{3}≈1.73$)( )| A. | 16平方米 | B. | 18平方米 | C. | 20平方米 | D. | 25平方米 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
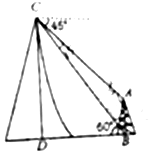 如图所示,在塔底B测得山顶C的仰角为60°,在山顶测得塔顶A的仰角为45°,已知塔高AB=20米,则山高DC=10(3+$\sqrt{3}$)米.
如图所示,在塔底B测得山顶C的仰角为60°,在山顶测得塔顶A的仰角为45°,已知塔高AB=20米,则山高DC=10(3+$\sqrt{3}$)米.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了解某地高中生的身高情况,研究小组在该地高中生中随机抽出30名高中生的身高统计成如图所示的茎叶图(单位:cm).
为了解某地高中生的身高情况,研究小组在该地高中生中随机抽出30名高中生的身高统计成如图所示的茎叶图(单位:cm).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com