
分析 (Ⅰ)利用已知条件推出数列{an}是等差数列,然后求解通项公式;
(Ⅱ)利用裂项消项法求解数列的和即可.
解答 解:(Ⅰ)∵$\frac{1}{{{a_{n+1}}}}=\frac{1}{{{a_n}+1}}$即an+1-an=1,
所以数列{an}是以1为首项,1为公差的等差数列,…2分
∴an=n…3分
(Ⅱ)${S_n}=\frac{n(n+1)}{2}$…5分
∴${T_n}=\frac{1}{S_1}+\frac{1}{S_2}+…+\frac{1}{S_n}=2[\frac{1}{1×2}+\frac{1}{2×3}+…+\frac{1}{n(n+1)}]$
=$2[(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})+…+(\frac{1}{n}-\frac{1}{n+1})]$…7分
=$2(1-\frac{1}{n+1})=\frac{2n}{n+1}$…9分.
点评 本题考查数列的通项公式的求法,数列求和的方法的应用,考查计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (-1,2) | C. | (1,2) | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
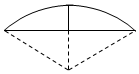 《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积=$\frac{1}{2}×$(弦×矢+矢2),弧田(如图)由圆弧和其所对弦围城,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角$\frac{2π}{3}$,半径为6米的弧田,按照上述经验公式计算所得弧田面积约是($\sqrt{3}≈1.73$)( )
《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积=$\frac{1}{2}×$(弦×矢+矢2),弧田(如图)由圆弧和其所对弦围城,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角$\frac{2π}{3}$,半径为6米的弧田,按照上述经验公式计算所得弧田面积约是($\sqrt{3}≈1.73$)( )| A. | 16平方米 | B. | 18平方米 | C. | 20平方米 | D. | 25平方米 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 把正整数按“f(x)”型排成了如图所示的三角形数表,第f(x)行有f(x)个数,对于第f(x)行按从左往右的顺序依次标记第1列,第2列,…,第f(x)列(比如三角形数表中12在第5行第4列,18在第6行第3列),则三角形数表中2017在( )
把正整数按“f(x)”型排成了如图所示的三角形数表,第f(x)行有f(x)个数,对于第f(x)行按从左往右的顺序依次标记第1列,第2列,…,第f(x)列(比如三角形数表中12在第5行第4列,18在第6行第3列),则三角形数表中2017在( )| A. | 第62行第2列 | B. | 第64行第64列 | C. | 第63行第2列 | D. | 第64行第1列 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com