
分析 (1)由3Sn=(n+2)an得3Sn-1=(n+1)an-1(n≥2),二式相减得3an=(n+2)an-(n+1)an-1f(x)
$\frac{a_n}{{{a_{n-1}}}}=\frac{n+1}{n-1}$(n≥2)叠乘得an=n(n+1);
(2)$\frac{1}{a_n}=\frac{1}{{n({n+1})}}$=$\frac{1}{n}-\frac{1}{n+1}$,${T_n}=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}$$+\frac{1}{2}-\frac{1}{4}+…+$$\frac{1}{n}-\frac{1}{n+1}=\frac{n}{n+1}$,
令$|{{T_n}-1}|=|{\frac{n}{n+1}-1}|$=$\frac{1}{n+1}<\frac{1}{10}$得n>9.
解答 解:(1)由3Sn=(n+2)an得3Sn-1=(n+1)an-1(n≥2),
二式相减得3an=(n+2)an-(n+1)an-1f(x)
∴$\frac{a_n}{{{a_{n-1}}}}=\frac{n+1}{n-1}$(n≥2)
∴$\frac{{{a_{n-1}}}}{{{a_{n-2}}}}=\frac{n}{n-2}$;…;$\frac{a_3}{a_2}=\frac{4}{2}$;$\frac{a_2}{a_1}=\frac{3}{1}$;a1=2
叠乘得an=n(n+1);
(2)$\frac{1}{a_n}=\frac{1}{{n({n+1})}}$=$\frac{1}{n}-\frac{1}{n+1}$,
∴${T_n}=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}$$+\frac{1}{2}-\frac{1}{4}+…+$$\frac{1}{n}-\frac{1}{n+1}=\frac{n}{n+1}$,
令$|{{T_n}-1}|=|{\frac{n}{n+1}-1}|$=$\frac{1}{n+1}<\frac{1}{10}$得n>9
故满足条件的M存在,集合M={n|n>9,n∈N*}.
点评 本题考查了数列的递推式,叠乘求通项,裂项求和,属于中档题.


 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±$\frac{1}{2}$x | B. | y=±$\sqrt{3}$x | C. | y=±2x | D. | y=±$\frac{{\sqrt{3}}}{3}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (-1,2) | C. | (1,2) | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
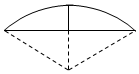 《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积=$\frac{1}{2}×$(弦×矢+矢2),弧田(如图)由圆弧和其所对弦围城,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角$\frac{2π}{3}$,半径为6米的弧田,按照上述经验公式计算所得弧田面积约是($\sqrt{3}≈1.73$)( )
《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积=$\frac{1}{2}×$(弦×矢+矢2),弧田(如图)由圆弧和其所对弦围城,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角$\frac{2π}{3}$,半径为6米的弧田,按照上述经验公式计算所得弧田面积约是($\sqrt{3}≈1.73$)( )| A. | 16平方米 | B. | 18平方米 | C. | 20平方米 | D. | 25平方米 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com