练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．a，b∈R，下列结论成立的是（　　）
    A．若a＜b，则ac＜bcB．若a＜b，c＜d，则ac＜bd
    C．若a＜b，则a-c＜b-cD．若a＜b，则an＜bn（n∈N*，n≥2）

    分析 A．取c≤0时，即可判断出正误；
    B．举反例：取a=-2，b=-1，c=-4，d=-3，即可判断出正误；
    C．利用不等式的基本性质即可判断出正误；
    D．举反例：取a=-2，b=-1，则a2＞b2，即可判断出正误．

    解答 解：A．c≤0时不成立；
    B．举反例：取a=-2，b=-1，c=-4，d=-3，则ab＞cd，因此不成立；
    C．∵a＜b，∴a-c＜b-c，正确；
    D．举反例：取a=-2，b=-1，则a2＞b2，因此不成立．
    故选：C．

    点评 本题考查了不等式的基本性质，考查了推理能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    19．给出命题：
    （1）垂直于同一直线的两个平面平行；
    （2）平行于同一直线的两个平面平行；
    （3）平行于两相交平面的直线一定平行于这两相交平面的交线；
    （4）平行于同一平面的两个平面平行；
    其中正确命题个数有（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．$C_n^0+C_n^1+…+C_n^r+…+C_n^n$=2n．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．已知$\overrightarrow{a}$=（-3，1），$\overrightarrow{b}$=（-1，2），若m$\overrightarrow{a}$-n$\overrightarrow{b}$=（10，0），（m，n∈R），则（　　）
    A．m=2，n=4B．m=3，n=-2C．m=4，n=2D．m=-4，n=-2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

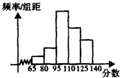    4．为了解某高三模拟考试学生数学学习情况，从该校参加质检的学生数学成绩中抽取一个样本，并分而5组，绘成如图所示的频率分布直方图，若第二组至第五组数据的频率分别为0.1，0.4，0.3，0.15，第一组数据的频数是2．
    （Ⅰ）估计该校高三学生质检数学成绩低于95分的概率，并求出样本容量．
    （Ⅱ）从样本中成绩在65分到95分之间的学生中任选两人，求至少有一人成绩在65分到80分之间的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．直线（2+λ）x+（λ-1）y-2λ-1=0经过的定点坐标为（1，1）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．要从已编号（01～06）的60枚最新研制的某型导弹中随机抽取6枚来进行发射试验，用系统抽样方法确定所选取的6枚导弹的编号可能是（　　）
    A．5，15，25，36，45，55B．2，4，8，16，32，48
    C．2，12，23，34，45，56D．3，13，23，33，43，53

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．某人射击一次，命中8-10环及不足8环的概率如下表：
    命中环数不足8环8环9环10环
    概率0•450•27x0•13
    则此人命中环数超过8环（不含8环）的概率是0.28．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．（本题只限理科学生做）
    已知Sn为数列{an}的前n项和，且${S_n}=2{a_n}+{n^2}-3n-2$，n=1，2，3…
    （Ⅰ）求证：数列{an-2n}为等比数列；
    （Ⅱ）设bn=an•cosnπ，求数列{bn}的前n项和Pn；
    （Ⅲ）设${c_n}=\frac{1}{{{a_n}-n}}$，数列{cn}的前n项和为Tn，求证：${T_n}＜\frac{5}{6}$．

    查看答案和解析>>

    同步练习册答案