
如图,在矩形ABCD中,AB=4,AD=2,E为AB的中点,现将△ ADE沿直线DE翻折成△A′DE,使平面A′DE⊥平面BCDE,F为线段A′D的中点.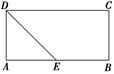
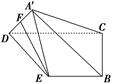
(1)求证:EF//平面A′BC;
(2)求直线A′B与平面A′DE所成角的正切值.
(1)要证明线面平行,只要通过证明线线平行来得到即可。
(2)
解析试题分析:解:(1)证明:取A′C的中点M,连结MF,MB,则FM∥DC,且FM= DC.
DC.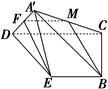
∵EB∥DC,且EB= DC,
DC,
∴FM∥EB且FM=EB.
∴四边形EBMF为平行四边形,
∴EF∥MB.
∵EF 平面A′BC,MB
平面A′BC,MB 平面A′BC,
平面A′BC,
∴EF∥平面A′BC. 4分
(2)过B作BO垂直于DE的延长线,O为垂足,连结A′O.
∵平面A′DE⊥平面BCDE,且平面A′DE∩平面BCDE=DE,
∴BO⊥平面A′DE,
∴∠BA′O就是直线A′B与平面A′DE所成的角. 7分
过A′作A′S⊥DE,S为垂足,
因为平面A′DE⊥平面BCDE,且平面A′DE∩平面BCDE=DE,
所以A′S⊥平面BCDE.
在Rt△A′SO中,A′S= ,SO=2
,SO=2 ,所以A′O=
,所以A′O=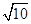 .
.
又BO= ,所以tan∠BA′O=
,所以tan∠BA′O=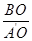 =
= =
= ,
,
故直线A′B与平面A′DE所成角的正切值为 . 10分
. 10分
考点:直线与平面平行的判定定理
点评:本题主要考查了直线与平面平行的判定定理与线面平行与线线平行的相互转化,还考查了直线与平面所成角的求解,要注意利用已知图形构造直角三角形进行求解.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:解答题
如图(1),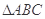 是等腰直角三角形,其中
是等腰直角三角形,其中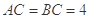 ,
,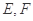 分别为
分别为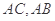 的中点,将
的中点,将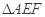 沿
沿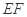 折起,点
折起,点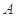 的位置变为点
的位置变为点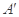 ,已知点
,已知点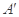 在平面
在平面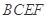 上的射影
上的射影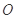 为
为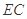 的中点,如图(2)所示.
的中点,如图(2)所示.
(1)求证: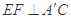 ;
;
(2)求三棱锥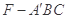 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
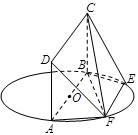
AB为圆O的直径,点E、F在圆上,AB//EF,矩形ABCD所在平面与圆O所在平面互相垂直,已知AB=2,BC=EF=1。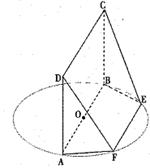
(I)求证:BF⊥平面DAF;
(II)求ABCD与平面CDEF所成锐二面角的某三角函数值;
(III)求多面体ABCDFE的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,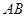 为圆
为圆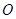 的直径,点
的直径,点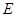 、
、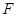 在圆
在圆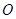 上,
上,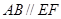 ,矩形
,矩形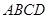 所在的平面与圆
所在的平面与圆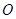 所在的平面互相垂直.已知
所在的平面互相垂直.已知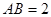 ,
,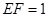 .
.
(Ⅰ)求证:平面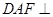 平面
平面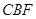 ;
;
(Ⅱ)求直线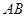 与平面
与平面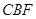 所成角的大小;
所成角的大小;
(Ⅲ)当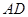 的长为何值时,平面
的长为何值时,平面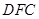 与平面
与平面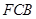 所成的锐二面角的大小为
所成的锐二面角的大小为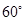 ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,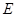 是以
是以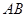 为直径的半圆上异于
为直径的半圆上异于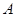 、
、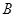 的点,矩形
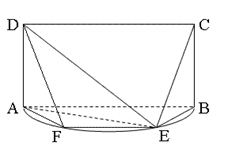
的点,矩形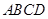 所在的平面垂直于该半圆所在的平面,且
所在的平面垂直于该半圆所在的平面,且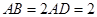 .
.
(Ⅰ)求证: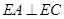 ;
;
(Ⅱ)设平面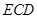 与半圆弧的另一个交点为
与半圆弧的另一个交点为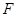 .
.
①试证: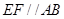 ;
;
②若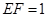 ,求三棱锥
,求三棱锥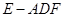 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,正方体ABCD—A1B1C1D1中,E为AB中点,F为正方形BCC1B1的中心.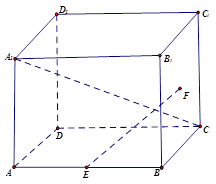
(1)求直线EF与平面ABCD所成角的正切值;
(2)求异面直线A1C与EF所成角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com