练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f（x）=（a>0,且a≠1）在上单调递减，且关于x的方程

    │f（x）│=2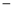x恰有两个不相等的实数解，则a的取值范围是

    （A）（0，] （B）[，] （C）[，]{} （D）[，）{}

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2016年全国普通高等学校招生统一考试理科数学（浙江卷精编版） 题型：填空题

    已知a＞b＞1.若logab+logba=，ab=ba，则a= ，b= .

    查看答案和解析>>

    科目：高中数学 来源：2016年全国普通高等学校招生统一考试文科数学（天津卷精编版） 题型：解答题

    如图，四边形ABCD是平行四边形，平面AED⊥平面ABCD，EF∥AB，AB=2，BC=EF=1，AE=，DE=3，∠BAD=60º，G为BC的中点.

    （Ⅰ）求证：FG平面BED；

    （Ⅱ）求证：平面BED⊥平面AED；

    （Ⅲ）求直线EF与平面BED所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源：2016年全国普通高等学校招生统一考试理科数学（天津卷精编版） 题型：解答题

    设函数x∈R，其中a,b∈R.

    （Ⅰ）求f（x）的单调区间；

    （Ⅱ）若f（x）存在极值点x0，且f（x1）= f（x0），其中x1≠x0，求证：x1+2x0=3；

    （Ⅲ）设a＞0,函数g（x）= |f（x）|,求证：g（x）在区间[0,2]上的最大值不小于.

    查看答案和解析>>

    科目：高中数学 来源：2016年全国普通高等学校招生统一考试理科数学（天津卷精编版） 题型：填空题

    已知f（x）是定义在R上的偶函数，且在区间（?，0）上单调递增.若实数a满足f（2|a-1|）＞f（），则a的取值范围是______.

    查看答案和解析>>

    科目：高中数学 来源：2016年全国普通高等学校招生统一考试理科数学（天津卷精编版） 题型：选择题

    在△ABC中，若，3，，则

    （A）1 （B）2 （C）3 （D）4

    查看答案和解析>>

    科目：高中数学 来源：2016年全国普通高等学校招生统一考试理科数学（山东卷精编版） 题型：解答题

    在如图所示的圆台中，AC是下底面圆O的直径，EF是上底面圆O的直径，FB是圆台的一条母线.

    （Ⅰ）已知G,H分别为EC，FB的中点，求证：GH∥平面ABC；

    （Ⅱ）已知EF=FB=AC=，AB=BC.求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源：2016年全国普通高等学校招生统一考试文科数学（四川卷精编版） 题型：解答题

    设函数f（x）=ax2–a–lnx，g（x）=，其中a∈R，e=2.718…为自然对数的底数.

    （Ⅰ）讨论f（x）的单调性；

    （Ⅱ）证明：当x＞1时，g（x）＞0；

    （Ⅲ）确定a的所有可能取值，使得f（x）＞g（x）在区间（1，+∞）内恒成立.

    查看答案和解析>>

    科目：高中数学 来源：2016年全国普通高等学校招生统一考试文科数学（上海卷精编版） 题型：解答题

    已知R，函数=.

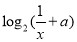    （1）当时，解不等式＞1；

    （2）若关于的方程+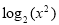=0的解集中恰有一个元素，求的值；

    （3）设＞0，若对任意，函数在区间上的最大值与最小值的差不超过1，求的取值范围.

    查看答案和解析>>

    同步练习册答案