
���� ������ƽ���������ߣ�ƽ�У��������ʾ�ɵ�2sinB•��2cos2$\frac{B}{2}$-1��+$\sqrt{3}$cos2B=0���������Ǻ�����ȱ任��Ӧ�û���ɵ�2sin��2B+$\frac{��}{3}$��=0�����BΪ��ǿ���B�������Ҷ������ɵý⣮
���������Ҷ����ɵ�ac=a2+c2-4�����û�������ʽ�ɵ�ac��4�����������������ʽ�����������ֵ��
��� ����������Ϊ12�֣�
�⣺����$\overrightarrow m$��$\overrightarrow n$��
⇒2sinB•��2cos2$\frac{B}{2}$-1��+$\sqrt{3}$cos2B=0������2�֣�
⇒sin2B+$\sqrt{3}$cos2B=0
⇒2sin��2B+$\frac{��}{3}$��=0��BΪ��ǣ�
⇒2B=$\frac{2��}{3}$
⇒B=$\frac{��}{3}$������4�֣�
��R=$\frac{b}{2sinB}=\frac{b}{\sqrt{3}}��$[1��2]����6�֣�
������cosB=$\frac{{a}^{2}+{c}^{2}-{2}^{2}}{2ac}$=$\frac{1}{2}$���ɵã�ac=a2+c2-4������8�֣�
��a2+c2��2ac����ac��4������10�֣�
��S��ABC=$\frac{1}{2}$acsinB��$\frac{1}{2}��4��\frac{\sqrt{3}}{2}$=$\sqrt{3}$��
��S��ABC�����ֵΪ$\sqrt{3}$������12�֣�
���� ������Ҫ������ƽ���������ߣ�ƽ�У��������ʾ�����Ǻ�����ȱ任��Ӧ�ã����Ҷ��������Ҷ�������������ʽ�������������ʽ�ڽ��������е�Ӧ�ã�������ת��˼������ν��˼���Ӧ�ã������е��⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��ֱ�Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֶ�����Ҫ���� | B�� | ��Ҫ�����ɷ����� | ||
| C�� | ��ֱ�Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
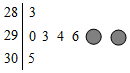 2016��2�£�ijƷ��������ij�����İ˼�4S����µ�������������ͳ�ƣ�ͳ�������羥Ҷͼ��ʾ�����ڹ�����Աʧ���������������ݣ���֪��Щ���ݵ�ƽ�����뷽��ֱ�Ϊ293��33.5�����ȱ�����������н�С������Ϊ1��
2016��2�£�ijƷ��������ij�����İ˼�4S����µ�������������ͳ�ƣ�ͳ�������羥Ҷͼ��ʾ�����ڹ�����Աʧ���������������ݣ���֪��Щ���ݵ�ƽ�����뷽��ֱ�Ϊ293��33.5�����ȱ�����������н�С������Ϊ1���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com