
分析 (Ⅰ)先求得f(x)的导数,f'(x)=3x2+2ax-(2a+3)=(x-1)(3x+2a+3),根据取得极大值点求得a的取值范围.
(Ⅱ)将方程f(x)=-$\frac{{{{({2a+3})}^2}}}{9}$看作两个函数,利用导数得到函数f(x)的大体图象,而函数y=-$\frac{{{{({2a+3})}^2}}}{9}$为一条平行于x轴的直线,利用交点个数说明a的值
(Ⅲ)依题意有:函数f(x)在区间[-2,2]上的最大值与最小值的差不大于m,转换思路,求最值.
解答 解:(Ⅰ)f(0)=0⇒c=0,f'(x)=3x2+2ax+b,f'(1)=0⇒b=-2a-3,…2分
∴f'(x)=3x2+2ax-(2a+3)=(x-1)(3x+2a+3),
由f'(x)=0⇒x=1或$x=-\frac{2a+3}{3}$
因为当x=1时取得极大值,所以$-\frac{2a+3}{3}>1⇒a<-3$,
所以a的取值范围是:(-∞,-3);…4分
(Ⅱ)由下表:
| x | x<1 | x=1 | $1<x<-\frac{2a+3}{3}$ | $x=-\frac{2a+3}{3}$ | $x>-\frac{2a+3}{3}$ |
| f'(x) | + | 0 | - | 0 | - |
| f(x) | 递增 | 极大值-a-2 | 递减 | 极小值$\frac{a+6}{27}{({2a+3})^2}$ | 递增 |
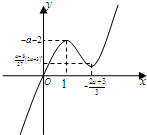
点评 本题主要考查利用导数求函数的单调区间和极值,利用函数得极值画函数图象的能力,属于中档题,高考经常涉及.


科目:高中数学 来源: 题型:选择题
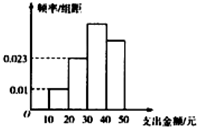 为了解学生在课外活动方面的支出情况,抽取了n个同学进行调查,结果显示这些学生的支出金额(单位:元)都在[10,50],其中支出金额在[30,50]的学生有134人,频率分布直方图如图所示,则n=( )
为了解学生在课外活动方面的支出情况,抽取了n个同学进行调查,结果显示这些学生的支出金额(单位:元)都在[10,50],其中支出金额在[30,50]的学生有134人,频率分布直方图如图所示,则n=( )| A. | 150 | B. | 160 | C. | 180 | D. | 200 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{π}{2}$,0) | B. | (0,1) | C. | (0,0) | D. | (-$\frac{π}{4}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a1d>0 | B. | a1d<0 | C. | d>0 | D. | d<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 锐角三角形 | B. | 直角三角形 | C. | 等腰三角形 | D. | 钝角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com