
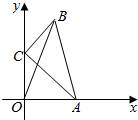
 在平面直角坐标系中,△ABC满足:∠C=90°,AC=2,BC=1,点A、C分别在x轴、y轴上,当点A从原点开始在x轴的正半轴上运动时,点C随着在y轴上运动.
在平面直角坐标系中,△ABC满足:∠C=90°,AC=2,BC=1,点A、C分别在x轴、y轴上,当点A从原点开始在x轴的正半轴上运动时,点C随着在y轴上运动.分析 (1)由题意画出图形,直接由三角形中的勾股定理得答案;
(2)结合图形,利用余弦定理求解;
(3)取AC中点D,连接OD,BD,则BD=$\sqrt{2}$,OD=1,利用三角形中两边之和大于第三边可得当O,D,B共线时,OB=OD+BD=1+$\sqrt{2}$最大,并进一步求得此时图形应满足什么条件.
解答 解:(1)当A在原点时,原点O到点B的距离OB=AB=$\sqrt{{2}^{2}+{1}^{2}}=\sqrt{5}$;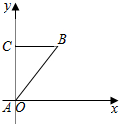
(2)当OA=OC时,∠OCB=135°,OC=$\frac{\sqrt{2}}{2}AC=\frac{\sqrt{2}}{2}×2=\sqrt{2}$,BC=1,
由余弦定理可得:OB=$\sqrt{(\sqrt{2})^{2}+{1}^{2}-2×1×\sqrt{2}cos135°}$=$\sqrt{3+2}=\sqrt{5}$;
(3)取AC中点D,连接OD,BD,则BD=$\sqrt{2}$,OD=1,
当O,D,B不共线时,OB<OD+BD=1+$\sqrt{2}$,
当O,D,B共线时,OB=OD+BD=1+$\sqrt{2}$,此时OB最大,
由CE=CB=1,可知∠CEB=45°,
又OE=CE,可得$∠ACO=\frac{45°}{2}=22.5°$.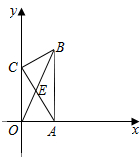
点评 本题考查两点间的距离公式的应用,考查了数形结合的解题思想方法,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com