
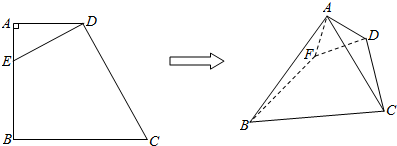
分析 (1)过A作AO⊥DE于点O,推导出AO⊥CD,CD⊥AD,由此能证明CD⊥AE.
(2)过B作BH⊥DE,交DE延长线于点H,连结AH,则∠BAH即为直线AB与平面ADE所成的角,由此能求出直线AB与平面ADE所成角.
解答 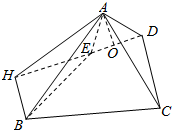 证明:(1)过A作AO⊥DE于点O,
证明:(1)过A作AO⊥DE于点O,
∵平面ADE⊥平面BCDE,平面ADE∩平面BCDE=DE,
∴AO⊥平面BCDE,∴AO⊥CD,
∵CD⊥AD,AD∩AO=A,∴CD⊥平面ADE,
∴CD⊥AE.
解:(2)过B作BH⊥DE,交DE延长线于点H,连结AH,
∵平面ADE⊥平面BCDE,平面ADE∩平面BCDE=DE,
∴BH⊥平面ADE,
∴∠BAH即为直线AB与平面ADE所成的角,
由(1)知CD⊥DE,
设AE=a,则BE=3-a,DE=$\sqrt{3+{a}^{2}}$,CE=$\sqrt{(3-{a}^{2})+12}$,
∵DE2+CD2=CE2,∴a=1,即AE=1,DE=2,BE=2,
∴△ADE≌△HBE,∴HB=$\sqrt{3}$,
∴在Rt△AHB中,∠BAH=45°,
即直线AB与平面ADE所成角为45°.
点评 本题考查异面直线垂直的证明,考查直线与平面所成角的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:选择题
| A. | 050 | B. | 051 | C. | 052 | D. | 053 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (13,49) | B. | [2,2+$\sqrt{13}$] | C. | [2,13] | D. | [4,22+6$\sqrt{13}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{5}$ | B. | $\frac{2\sqrt{2}}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
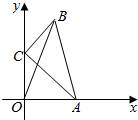 在平面直角坐标系中,△ABC满足:∠C=90°,AC=2,BC=1,点A、C分别在x轴、y轴上,当点A从原点开始在x轴的正半轴上运动时,点C随着在y轴上运动.
在平面直角坐标系中,△ABC满足:∠C=90°,AC=2,BC=1,点A、C分别在x轴、y轴上,当点A从原点开始在x轴的正半轴上运动时,点C随着在y轴上运动.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com