练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．若从区间（0，e）（e为自然对数的底数，e=2.71828…）内随机选取两个数，则这两个数之积小于e的概率为（　　）
    A．$\frac{2}{e}$B．$\frac{1}{e}$C．1-$\frac{2}{e}$D．1-$\frac{1}{e}$

    分析 由题意，$\left\{\begin{array}{l}{0＜x＜e}\\{0＜y＜e}\end{array}\right.$，区域面积为e2，这两个数之积小于e，$\left\{\begin{array}{l}{0＜x＜e}\\{0＜y＜e}\\{xy＜e}\end{array}\right.$，区域面积为e+${∫}_{1}^{e}\frac{e}{x}dx$=2e，即可得出结论．

    解答 解：由题意，$\left\{\begin{array}{l}{0＜x＜e}\\{0＜y＜e}\end{array}\right.$，区域面积为e2，
    这两个数之积小于e，$\left\{\begin{array}{l}{0＜x＜e}\\{0＜y＜e}\\{xy＜e}\end{array}\right.$，区域面积为e+${∫}_{1}^{e}\frac{e}{x}dx$=2e，
    ∴这两个数之积小于e的概率为$\frac{2}{e}$，
    故选A．

    点评 本题主要考查几何概型的概率计算，根据条件求出对应的区域面积是解决本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    18．已知函数$f（x）=x-alnx+a+\frac{b}{x}$．
    （1）若曲线y=f（x）在点（1，f（1））处的切线过点（4，-2），且x=2时，y=f（x）有极值，求实数a，b的值；
    （2）若函数g（x）=x•f（x）在区间$[\frac{1}{e}，{e^2}]$上单调递增，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．若圆x2+y2-x+my-4=0关于直线x-y=0对称，动点P（a，b）在不等式组$\left\{\begin{array}{l}x+y-2≤0\\ x+my≥0\\ y≥0\end{array}\right.$表示的平面区域内部及边界上运动，则$z=\frac{b-2}{a-1}$的取值范围是（-∞，-2]∪[2，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知函数$f（x）=（1-k）x+\frac{1}{e^x}$．
    （Ⅰ）求函数f（x）的单调区间；
    （Ⅱ）当k=0时，过点A（0，t）存在函数曲线f（x）的切线，求t的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

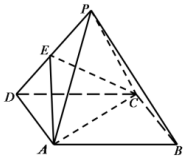    3．如图，四棱锥P-ABCD中，底面ABCD是平行四边形，且平面PAC⊥平面ABCD，E为PD的中点，PA=PC，AB=2BC=2，∠ABC=60°．
    （Ⅰ）求证：PB∥平面ACE；
    （Ⅱ）求证：平面PBC⊥平面PAC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

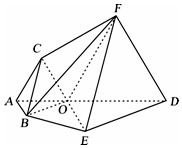    13．如图，ABEDEFC为多面体，平面ABED⊥平面ACED，点O在线段AD上，OA=1，OD=2，△OAB，△OAC，△ODE，△ODF都是正三角形．
    （1）证明：平面OCB∥平面EFD；
    （2）求直线OD与平面OEF所成角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．关于函数的对称性有如下结论：对于给定的函数y=f（x），x∈D，如果对于任意的x∈D都有f（a+x）+f（a-x）=2b成立（a，b为常数），则函数f（x）关于点（a，b）对称．
    （1）用题设中的结论证明：函数f（x）=$\frac{-2x+1}{x-3}$关于点（3，-2）；
    （2）若函数f（x）既关于点（2，0）对称，又关于点（-2，1）对称，且当x∈（2，6）时，f（x）=2x+3x，求：
    ①f（-5）的值；
    ②当x∈（8k-2，8k+2），k∈Z时，f（x）的表达式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．若实数x，y满足$\left\{\begin{array}{l}x-y+1≤0\\ x＞0\\ y≤2\end{array}\right.$，则$\frac{2y}{2x+1}$的最小值是$\frac{4}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．已知函数g（x）=a-x2（$\frac{1}{e}$≤x≤e，e为自然底数）与h（x）=2lnx的图象上存在关于x轴对称的点，则实数a的取值范围是[1，e2-2]．

    查看答案和解析>>

    同步练习册答案