
分析 (1)根据题设中的结论证明即可,
(2)由题意可得f(x+8)=f(x)-2,①代值计算即可,
②由f(x)=f(x-8)-2=f(x-8×2)-2×2=f(x-8×3)-2×3=…=f(x-8k)-2k,然后代值计算即可.
解答 解:(1)f(x)=$\frac{-2x+1}{x-3}$的定义域为{x|x≠3},对任意x≠3有f(3-x)+f(3-x)=(-2-$\frac{5}{x}$)+(-2-$\frac{5}{-x}$)=-4,
∴函数f(x)=$\frac{-2x+1}{x-3}$关于点(3,-2);
(2)函数f(x)关于点(2,0)对称,
∴f(2+x)+f(2-x)=0,
即f(x)+f(4-x)=0,
又关于点(-2,1)对称,
∴f(-2+x)+f(-2-x)=2,
即f(x)+f(-4-x)=2,
∴f(-4-x)=2+f(4-x),
即f(x+8)=f(x)-2,
①f(-5)=f(3)+2=23+3×3+2=19,
②x∈(8k-2,8k+2),x-8k∈(-2,2),4-(x-8k)∈(2,6),
∴f(x)=f(x-8)-2=f(x-8×2)-2×2=f(x-8×3)-2×3=…=f(x-8k)-2k,
又由f(t)=-f(4-t),
∴f(x)=f(x-8k)-2k=-f[4-(x-8k)]-2k=-[24-(x-8k)+3(4-(x-8k))]-2k,
∴即当x∈(8k-2,8k+2),k∈Z时,f(x)=-24-x+8k+3x-26k-12
点评 本题考查了抽象函数和新定义的应用,关键是掌握新定义的用法,属于中档题.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0,1,2} | B. | {-1,-2} | C. | {1,2} | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{e}$ | B. | $\frac{1}{e}$ | C. | 1-$\frac{2}{e}$ | D. | 1-$\frac{1}{e}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
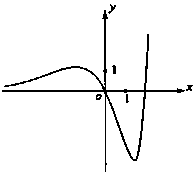
| A. | a=1,b=2 | B. | a=1,b=-2 | C. | a=-1,b=2 | D. | a=-1,b=-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com