
| A. | $\sqrt{3}$ | B. | $2\sqrt{2}$ | C. | $\sqrt{7}$ | D. | $\sqrt{23}$ |
分析 由已知的等式求出向量$\overrightarrow a,\overrightarrow b$的数量积,然后通过求$|{\overrightarrow a-\overrightarrow b}|$2再求模.
解答 解:因为向量$\overrightarrow a,\overrightarrow b$满足$|{\overrightarrow a}|=2,|{\overrightarrow b}|=3,\overrightarrow a•({\overrightarrow b-\overrightarrow a})=1$,所以$\overrightarrow{a}•\overrightarrow{b}=1+{\overrightarrow{a}}^{2}=5$,
则$|{\overrightarrow a-\overrightarrow b}|$=$\sqrt{{\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}+2\overrightarrow{a}•\overrightarrow{b}}$=$\sqrt{4+9-5}=2\sqrt{2}$;
故选B
点评 本题考查了平面向量数量积公式的运用以及模的计算;属于常规题型.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 充要 | B. | 充分非必要 | ||
| C. | 必要非充分 | D. | 既非充分也非必要 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 11,45 | B. | 5,45 | C. | 3,5 | D. | 5,15 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 高二年级有21个班,1班51人,2班53人,三班52人,由此推测各班都超过50人 | |
| B. | 猜想数列$\frac{1}{1×2}$,$\frac{1}{2×3}$,$\frac{1}{3×4}$,…的通项公式为an=$\frac{1}{n(n+1)}$(n∈N+) | |
| C. | 半径为r的圆的面积S=πr2,则单位圆的面积S=π | |
| D. | 由平面三角形的性质,推测空间四面体性质 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\sqrt{3}$ | B. | $-\frac{{\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
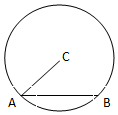
| A. | 8 | B. | -8 | C. | 4 | D. | -4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com