
| A. | $3\sqrt{6}$ | B. | $4\sqrt{6}$ | C. | $6\sqrt{6}$ | D. | 12$\sqrt{6}$ |
分析 根据向量加法的几何意义得出P点轨迹,利用正弦定理解出AB,得出△ABC的面积,从而求出围成封闭区域的面积.
解答 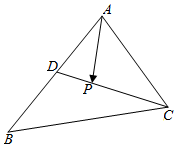 解:取AB的中点D,连结CD.则$\overrightarrow{AD}=\frac{1}{2}\overrightarrow{AB}$.
解:取AB的中点D,连结CD.则$\overrightarrow{AD}=\frac{1}{2}\overrightarrow{AB}$.
∵$\overrightarrow{AP}$=$\frac{λ}{2}$$\overrightarrow{AB}$+(1-λ)$\overrightarrow{AC}$=$λ\overrightarrow{AD}$+(1-λ)$\overrightarrow{AC}$.
∴C,D,P三点共线.
∴P点轨迹为直线CD.
在△ABC中,sinA=$\sqrt{1-co{s}^{2}A}$=$\frac{2\sqrt{6}}{5}$.cosC=$\sqrt{1-si{n}^{2}C}$=$\frac{5}{7}$.
由正弦定理得$\frac{BC}{sinA}=\frac{AB}{sinC}$,即$\frac{7}{\frac{2\sqrt{6}}{5}}=\frac{AB}{\frac{2\sqrt{6}}{7}}$,解得AB=5.
∴sinB=sin(A+C)=sinAcosC+cosAsinC=$\frac{2\sqrt{6}}{5}×\frac{5}{7}+\frac{1}{5}×\frac{2\sqrt{6}}{7}$=$\frac{12\sqrt{6}}{35}$.
∴S△ABC=$\frac{1}{2}AB×BC×sinB$=$\frac{1}{2}×5×7×\frac{12\sqrt{6}}{35}$=6$\sqrt{6}$.
∴S△ACD=$\frac{1}{2}$S△ABC=3$\sqrt{6}$.
故选:A.
点评 本题考查了平面向量线性运算的几何意义,正弦定理解三角形,属于中档题.


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=\frac{1}{x}$ | B. | y=lgx | C. | y=|x|-1 | D. | $y={({\frac{1}{2}})^{lnx}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | [0,1) | C. | [-1,1] | D. | [-1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
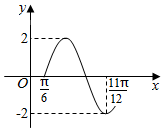 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,则f(x)的递增区间为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,则f(x)的递增区间为( )| A. | $({-\frac{π}{12}+2kπ,\frac{5π}{12}+2kπ})$,k∈Z | B. | $({-\frac{π}{12}+kπ,\frac{5π}{12}+kπ})$,k∈Z | ||
| C. | $({-\frac{π}{6}+2kπ,\frac{5π}{6}+2kπ})$,k∈Z | D. | $({-\frac{π}{6}+kπ,\frac{5π}{6}+kπ})$,k∈Z |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com