
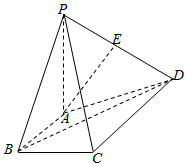
 如图,四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=$\frac{π}{2}$,AB=BC=1,CD=2,PA⊥平面ABCD,E是PD的中点.
如图,四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=$\frac{π}{2}$,AB=BC=1,CD=2,PA⊥平面ABCD,E是PD的中点.分析 (1)取PC中点F,连结EF、BF,推导出四边形ABFE为平行四边形,从而AE∥BF,由此能证明AE∥平面PBC.
(2)AE与直线BC所成角为$\frac{π}{3}$,延长BA一倍到H,连结DH,再作HG⊥BP,连结DG,∠DGH是二面角D-PB-A的平面角,由此能求出二面角D-PB-A平面角的余弦值.
解答 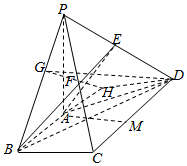 证明:(1)取PC中点F,连结EF、BF,
证明:(1)取PC中点F,连结EF、BF,
∴△PCD中,EF$\underset{∥}{=}$$\frac{1}{2}CD$,AB$\underset{∥}{=}$$\frac{1}{2}CD$,
∴EF$\underset{∥}{=}$AB,
∴四边形ABFE为平行四边形,
∵AE∥BF,AE?平面PBC,BF?平面PBC,
∴AE∥平面PBC.
解:(2)AE与直线BC所成角为$\frac{π}{3}$,$∠FBC=\frac{π}{3}$,
∴BP=$\sqrt{3}$,∴PA=$\sqrt{2}$,
延长BA一倍到H,连结DH,再作HG⊥BP,连结DG,
则∠DGH是二面角D-PB-A的平面角,
DH=1,FG×$\sqrt{3}=2×\sqrt{2}$,HG=$\frac{2\sqrt{2}}{\sqrt{3}}$,
∴tan∠DGH=$\frac{DH}{HG}=\frac{\sqrt{3}}{2\sqrt{2}}=\frac{\sqrt{6}}{4}$,
∴cos∠DGH=$\frac{2\sqrt{22}}{11}$$\frac{2\sqrt{11}}{11}$.
∴二面角D-PB-A平面角的余弦值为$\frac{2\sqrt{22}}{11}$.
点评 本题考查线面平行的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,-4] | B. | [-2,+∞) | C. | [-4,-2] | D. | (-∞,-4]∪[-2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
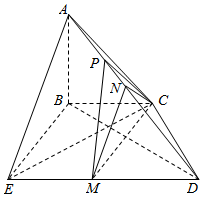 如图所示,平面ABC⊥平面BCDE,BC∥DE,$BC=\frac{1}{2}DE=2$,BE=CD=2,AB⊥BC,M,N分别为DE,AD中点.
如图所示,平面ABC⊥平面BCDE,BC∥DE,$BC=\frac{1}{2}DE=2$,BE=CD=2,AB⊥BC,M,N分别为DE,AD中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在多面体ABC-DEFG中,平面ABC∥平面DEFG,AC∥GF,且△ABC是边长为2的正三角形,DEFG是边长为4的正方形,M,N分别是AD,BE的中点,则MN=( )
如图,在多面体ABC-DEFG中,平面ABC∥平面DEFG,AC∥GF,且△ABC是边长为2的正三角形,DEFG是边长为4的正方形,M,N分别是AD,BE的中点,则MN=( )| A. | $\sqrt{7}$ | B. | 4 | C. | $\sqrt{19}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
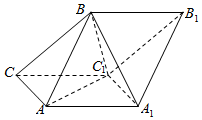 如图,斜三棱柱ABC-A1B1C1的侧面AA1C1C是菱形,侧面ABB1A1⊥侧面AA1C1C,A1B=AB=AA1=2,△AA1C1的面积为$\sqrt{3}$,且∠AA1C1为锐角.
如图,斜三棱柱ABC-A1B1C1的侧面AA1C1C是菱形,侧面ABB1A1⊥侧面AA1C1C,A1B=AB=AA1=2,△AA1C1的面积为$\sqrt{3}$,且∠AA1C1为锐角.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示为某几何体的三视图,其中正视图和左视图都是腰长为1的等腰直角三角形,该几何体的体积为V1,其外接球的体积为V2,则$\frac{{V}_{2}}{{V}_{1}}$的值为( )
如图所示为某几何体的三视图,其中正视图和左视图都是腰长为1的等腰直角三角形,该几何体的体积为V1,其外接球的体积为V2,则$\frac{{V}_{2}}{{V}_{1}}$的值为( )| A. | $\sqrt{3}$π | B. | 2$\sqrt{3}$π | C. | 3$\sqrt{3}$π | D. | $\frac{3\sqrt{3}π}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com