
已知抛物线 :
:
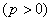 ,直线交此抛物线于不同的两个点
,直线交此抛物线于不同的两个点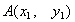 、
、 .
.
(1)当直线过点 时,证明
时,证明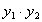 为定值;
为定值;
(2)如果直线过点 ,过点
,过点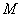 再作一条与直线垂直的直线
再作一条与直线垂直的直线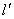 交抛物线
交抛物线 于两个不同点
于两个不同点 、
、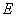 .设线段
.设线段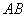 的中点为
的中点为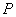 ,线段
,线段 的中点为
的中点为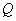 ,记线段
,记线段 的中点为
的中点为 .问是否存在一条直线和一个定点,使得点
.问是否存在一条直线和一个定点,使得点 到它们的距离相等?若存在,求出这条直线和这个定点;若不存在,请说明理由.
到它们的距离相等?若存在,求出这条直线和这个定点;若不存在,请说明理由.
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com