
分析 (1)设椭圆的左焦点为F′,则|CF|+|CF′|=4=2a,求出a的值,再原点O到直线DF的距离为$\frac{\sqrt{3}}{2}$,直线DF的方程为$\frac{x}{c}$+$\frac{y}{b}$=1可得到c,b的值,进而得到椭圆的方程;
(2)假设存在直线满足条件,设直线方程为y=k(x-2)+1,然后与椭圆方程联立消去y得到一元二次方程,且方程一定有两根,故应△大于0得到k的范围,进而可得到两根之和、两根之积的表达式,再由$\overrightarrow{O{P}^{2}}$=4$\overrightarrow{PA}$•$\overrightarrow{PB}$可确定k的值,从而得解.
解答 解:(1)设椭圆的左焦点为F′,则|CF|+|CF′|=4=2a,
∴a=2.
∵原点O到直线DF的距离为$\frac{\sqrt{3}}{2}$,直线DF的方程为$\frac{x}{c}$+$\frac{y}{b}$=1,
∴$\frac{1}{\sqrt{\frac{1}{{c}^{2}}+\frac{1}{{b}^{2}}}}$=$\frac{\sqrt{3}}{2}$,
∴bc=$\sqrt{3}$,
∵a>b>c>0,
∴b=$\sqrt{3}$,c=1,
∴椭圆E的方程$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1;
(2)若存在直线l满足条件,由题意可设直线l的方程为y=k(x-2)+1,
联立$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1,得(3+4k2)x2-8k(2k-1)x+16k2-16k-8=0.
∵直线l与椭圆C相交于不同的两点A,B,
设A,B两点的坐标分别为(x1,y1),(x2,y2),
所以△=[-8k(2k-1)]2-4•(3+4k2)•(16k2-16k-8)>0.
整理得32(6k+3)>0.
解得k>-$\frac{1}{2}$,
x1+x2=$\frac{8k(2k-1)}{3+4{k}^{2}}$,x1x2=$\frac{16{k}^{2}-16k-8}{3+4{k}^{2}}$
∵$\overrightarrow{O{P}^{2}}$=4$\overrightarrow{PA}$•$\overrightarrow{PB}$,即4(x1-2)(x2-2)+(y1-1)(y2-1)=5,
∴(x1-2)(x2-2)(1+k2)=$\frac{5}{4}$.
即[x1x2-2(x1+x2)++4](1+k2)=$\frac{5}{4}$.
∴($\frac{16{k}^{2}-16k-8}{3+4{k}^{2}}$-2×$\frac{8k(2k-1)}{3+4{k}^{2}}$+4](1+k2)=$\frac{5}{4}$.
解得k=±$\frac{1}{2}$.
∵A,B为不同的两点,
∴k=$\frac{1}{2}$.
于是存在直线l满足条件,其方程为y=$\frac{1}{2}$x.
点评 本题主要考查椭圆的基本性质和直线与椭圆的综合题.直线与圆锥曲线的综合题是高考的重点题型,是压轴题.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:高中数学 来源: 题型:解答题
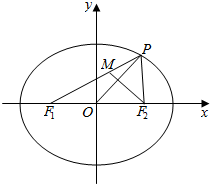 如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点为F1、F2,P是椭圆上一点,M在PF1上,且满足$\overrightarrow{{F_1}M}=λ\overrightarrow{MP}$(λ∈R),PO⊥F2M,O为坐标原点.
如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点为F1、F2,P是椭圆上一点,M在PF1上,且满足$\overrightarrow{{F_1}M}=λ\overrightarrow{MP}$(λ∈R),PO⊥F2M,O为坐标原点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com