Question

10．已知向量$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，对于任意点M，点M关于A点的对称点为S，点S关于B点的对称点为N．
（1）用$\overrightarrow{a}$，$\overrightarrow{b}$表示$\overrightarrow{MN}$；
（2）用|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=2，|$\overrightarrow{MN}$|∈[2$\sqrt{3}$，2$\sqrt{7}$]，求$\overrightarrow{a}$与$\overrightarrow{b}$的夹角θ的取值范围．

Answer 1

分析 （1）由题意可知AB是△SMN的中位线，故$\overrightarrow{MN}=2\overrightarrow{AB}$．
（2）由MN的范围得出AB的范围，两边平方得出$\overrightarrow{OA}•\overrightarrow{OB}$的范围．

解答 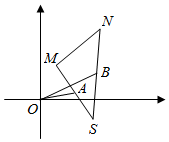解：（1）∵A是SM的中点，B是SN的中点，
∴AB是△SMN的中位线，∴$\overrightarrow{MN}$=2$\overrightarrow{AB}$=2（$\overrightarrow{OB}-\overrightarrow{OA}$）=2$\overrightarrow{b}$-2$\overrightarrow{a}$．
（2）∵|$\overrightarrow{MN}$|∈[2$\sqrt{3}$，2$\sqrt{7}$]，∴$\sqrt{3}$≤|$\overrightarrow{AB}$|≤$\sqrt{7}$．
∴3≤（$\overrightarrow{OB}-\overrightarrow{OA}$）²≤7，
即3≤1+4-2$\overrightarrow{OA}•\overrightarrow{OB}$≤7，解得-1≤$\overrightarrow{OA}•\overrightarrow{OB}$≤1．
∵$\overrightarrow{OA}•\overrightarrow{OB}$=|$\overrightarrow{a}$||$\overrightarrow{b}$|cosθ=2cosθ，
∴-$\frac{1}{2}$≤cosθ≤$\frac{1}{2}$．∵θ∈[0，π]，
∴$\frac{π}{3}$≤θ≤$\frac{2π}{3}$．

点评 本题考查了平面向量的数量积运算，向量的几何意义，属于基础题．