
分析 由已知中f(x)=$\sqrt{1+x}$,当π<θ<$\frac{5π}{4}$时,将x=sin2θ和x=cos2θ代入,结合二倍角公式,及$\sqrt{{x}^{2}}=\left|x\right|$化简可得答案.
解答 解:∵f(x)=$\sqrt{1+x}$,π<θ<$\frac{5π}{4}$,
∴f(sin2θ)-$\sqrt{2}$f(cos2θ)=$\sqrt{1+sin2θ}$-$\sqrt{2}$$\sqrt{1+cos2θ}$=$\sqrt{(sinθ+cosθ)^{2}}$-$\sqrt{2}$$\sqrt{2{cos}^{2}θ}$=|sinθ+cosθ|-2|cosθ|=-sinθ-cosθ+2cosθ=cosθ-sinθ,
故答案为:cosθ-sinθ
点评 本题考查的知识点是函数求值,二倍角公式,三角函数的符号,难度中档.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
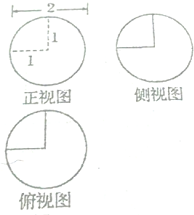
| A. | 4π | B. | $\frac{15π}{4}$ | C. | 5π | D. | $\frac{17π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 共线 | B. | 不共线 | C. | 共线且同向 | D. | 不一定共线 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com