Question

4．已知x，y∈R，且$\left\{\begin{array}{l}{\sqrt{3}x+y≤4\sqrt{3}}\\{\sqrt{3}x-y≥0}\\{y≥0}\end{array}\right.$，则存在θ∈R，使得xcosθ+ysinθ+1=0成立的P（x，y）构成的区域面积为（　　）

• A． 4$\sqrt{3}$-$\frac{π}{6}$
• B． 4$\sqrt{3}$-$\frac{π}{3}$
• C． $\frac{π}{2}$
• D． $\frac{\sqrt{3}}{4}$+$\frac{π}{6}$

Answer 1

分析 作出不等式组对应的平面区域，求解xcosθ+ysinθ+1=0成立的等价条件，利用数形结合求出对应的面积即可得到结论．

解答 解：作出不等式组对应的平面区域如图：对应的区域为三角形OAB，
若存在θ∈R，使得xcosθ+ysinθ+1=0成立，
则$\sqrt{{x}^{2}+{y}^{2}}$（$\frac{x}{\sqrt{{x}^{2}+{y}^{2}}}$cosθ+$\frac{y}{\sqrt{{x}^{2}+{y}^{2}}}$sinθ）=-1，
令sinα=$\frac{x}{\sqrt{{x}^{2}+{y}^{2}}}$，则cosθ=$\frac{y}{\sqrt{{x}^{2}+{y}^{2}}}$，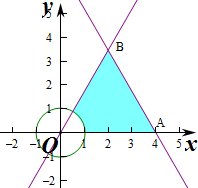
则方程等价为$\sqrt{{x}^{2}+{y}^{2}}$sin（α+θ）=-1，
即sin（α+θ）=-$\frac{1}{\sqrt{{x}^{2}+{y}^{2}}}$，
∵存在θ∈R，使得xcosθ+ysinθ+1=0成立，
∴|-$\frac{1}{\sqrt{{x}^{2}+{y}^{2}}}$|≤1，即x²+y²≥1，
则对应的区域为单位圆的外部，
由$\left\{\begin{array}{l}{\sqrt{3}x+y=4\sqrt{3}}\\{\sqrt{3}x-y=0}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=2}\\{y=2\sqrt{3}}\end{array}\right.$，即B（2，2$\sqrt{3}$），
A（4，0），则三角形OAB的面积S=$\frac{1}{2}×4$×$2\sqrt{3}$=4$\sqrt{3}$，
直线y=$\sqrt{3}$x的倾斜角为$\frac{π}{3}$，
则∠AOB=$\frac{π}{3}$，即扇形的面积为$\frac{π}{6}$，
则P（x，y）构成的区域面积为S=4$\sqrt{3}$-$\frac{π}{6}$，
故选：A

点评 本题主要考查线性规划的应用，根据条件作出对应的图象，求出对应的面积是解决本题的关键．综合性较强．