Question

4．作出下列函数的图象，并根据图象指出函数的值域．
（1）y=$\frac{x|1-x|}{1{-x}^{2}}$；
（2）y=$\frac{{e}^{x}}{x-1}$．

Answer 1

分析 （1）化简函数的解析式，然后画出函数的图象即可．
（2）利用函数的导数，判断函数的单调性以及函数的最值，然后画出函数的图象．

解答 -∞解：（1）y=$\frac{x|1-x|}{1{-x}^{2}}$=$\left\{\begin{array}{l}{\frac{x}{1+x}，x＞1}\\{-\frac{x}{1+x}，x＜1}\end{array}\right.$，
函数的图象如图：函数的值域为：（-∞，$\frac{1}{2}$）∪（1，+∞）．
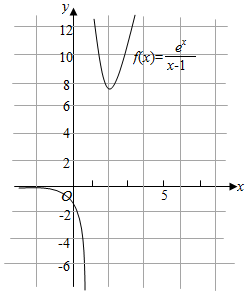
（2）y=$\frac{{e}^{x}}{x-1}$．可得y′=$\frac{（x-2）{e}^{x}}{（x-1）^{2}}$，x∈（-∞，1）函数是减函数；
x∈（1，2），函数是减函数，y≥e²，x∈（2，+∞）时，函数是增函数．图象如图：
函数的值域为：（-∞，0）∪[e²，+∞）．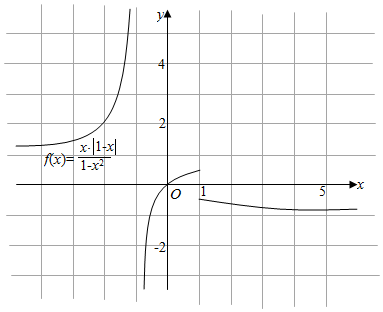

点评 本题考查函数的图象的画法，函数的单调性以及函数的值域的求法，考查数形结合以及计算能力．