
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)当![]() ,
,![]() 时,求函数
时,求函数![]() 的最小值;
的最小值;
(2)当![]() ,
,![]() 时,求证方程
时,求证方程![]() 在区间
在区间![]() 上有唯一实数根;
上有唯一实数根;
(3)当![]() 时,设
时,设![]() 是
是![]() 函数两个不同的极值点,证明:
函数两个不同的极值点,证明:![]() .
.
【答案】(1)![]() (2)见解析(3)见解析
(2)见解析(3)见解析
【解析】
(1)构造新函数y=![]() ,求导判断单调性,得出最小值e.(2)变量分离a=-
,求导判断单调性,得出最小值e.(2)变量分离a=-![]() =h(x),根据函数的单调性求出函数h(x)的最小值,利用a的范围证明在区间(0,2)上有唯一实数根;(3)求出
=h(x),根据函数的单调性求出函数h(x)的最小值,利用a的范围证明在区间(0,2)上有唯一实数根;(3)求出![]() ,问题转化为证
,问题转化为证![]() ,令x1﹣x2=t,得到t<0,根据函数的单调性证明即可.
,令x1﹣x2=t,得到t<0,根据函数的单调性证明即可.
(1)当![]() =0,
=0,![]() 时,
时,![]() =
=![]() ,求导y’=
,求导y’=![]() =0的根x=1
=0的根x=1
所以y在(-![]() ),(0,1)递减,在(1,+
),(0,1)递减,在(1,+![]() )递增,
)递增,
所以y![]() =e
=e
(2)![]() +
+![]() =0,所以a=-
=0,所以a=-![]() =h(x)
=h(x)
H’(x)=-![]() =0的根x=2
=0的根x=2
则h(x)在(0,2)上单调递增,在(2,+∞)上单调递减,
所以h(2)是y=h(x)的极大值即最大值,即![]()
所以函数f(x)在区间(0,2)上有唯一实数根;
(3)![]() =
= ![]() -
-![]()
F’(x)![]() -2ax-a=0的两根是
-2ax-a=0的两根是![]() ,
,![]()
∵x1,x2是函数F(x)的两个不同极值点(不妨设x1<x2),
∴a>0(若a≤0时,f'(x)>0,即F(x)是R上的增函数,与已知矛盾),
且F'(x1)=0,F'(x2)=0.∴![]() ,
,![]() …
…
两式相减得: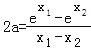 ,…
,…
于是要证明![]() ,即证明
,即证明 ,两边同除以
,两边同除以![]() ,
,
即证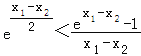 ,即证
,即证![]() ,即证
,即证![]() ,
,
令x1﹣x2=t,t<0.即证不等式![]() ,当t<0时恒成立.
,当t<0时恒成立.
设![]() ,∴
,∴![]() =
=![]()
设![]() ,∴
,∴![]() ,
,
当t<0,h'(t)<0,h(t)单调递减,
所以h(t)>h(0)=0,即![]() ,
,
∴φ'(t)<0,∴φ(t)在t<0时是减函数.
∴φ(t)在t=0处取得极小值φ(0)=0.
∴φ(t)>0,得证.
∴![]() .
.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
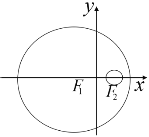
【题目】如图,已知圆![]() 的方程为
的方程为![]() ,圆
,圆![]() 的方程为
的方程为![]() ,若动圆
,若动圆![]() 与圆
与圆![]() 内切,与圆
内切,与圆![]() 外切.
外切.
(Ⅰ)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过直线![]() 上的点
上的点![]() 作圆
作圆![]() 的两条切线,设切点分别是
的两条切线,设切点分别是![]() ,
,![]() ,若直线
,若直线![]() 与轨迹
与轨迹![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率
,离心率![]() ,且椭圆的短轴长为2.
,且椭圆的短轴长为2.
(1)球椭圆的标准方程;
(2)已知直线![]() 过右焦点
过右焦点![]() ,且它们的斜率乘积为
,且它们的斜率乘积为![]() ,设
,设![]() 分别与椭圆交于点
分别与椭圆交于点![]() 和
和![]() .
.
①求![]() 的值;
的值;
②设![]() 的中点
的中点![]() ,
,![]() 的中点为,求
的中点为,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题,其中正确的序号是________(写出所有正确命题的序号).
①已知集合![]() ,
,![]() ,则映射
,则映射![]() 中满足
中满足![]() 的映射共有
的映射共有![]() 个;
个;
②函数![]() 的图象关于
的图象关于![]() 对称的函数解析式为
对称的函数解析式为![]() ;
;
③若函数![]() 的值域为
的值域为![]() ,则实数
,则实数![]() 的取值范围是
的取值范围是![]() ;
;
④已知函数![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() ,则
,则![]() 的值等于
的值等于![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】20名高二学生某次数学考试成绩(单位:分)的频率分布直方图如图:
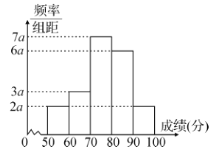
(1)求频率分布直方图中![]() 的值;
的值;
(2)分别求出成绩落在![]() 与
与![]() 中的学生人数;
中的学生人数;
(3)从成绩在![]() 的学生中任选2人,求此2人的成绩都在
的学生中任选2人,求此2人的成绩都在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2-2ax-1+a,a∈R.
(1)若a=2,试求函数y=![]() (x>0)的最小值;
(x>0)的最小值;
(2)对于任意的x∈[0,2],不等式f(x)≤a成立,试求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我国经济的发展,居民的储蓄存款逐年增长。设某地区城乡居民人民币储蓄存款![]() (单位:亿元)的数据如下:
(单位:亿元)的数据如下:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
储蓄存款 | 3.4 | 3.6 | 4.5 | 4.9 | 5.5 | 6.1 | 7.0 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)2018年城乡居民储蓄存款前五名中,有三男和两女。现从这5人中随机选出2人参加某访谈节目,求选中的2人性别不同的概率。
附:回归直线的斜率和截距的最小二乘估计公式分别为: ,
,![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,圆
,圆![]() 经过椭圆
经过椭圆![]() 的两个焦点和两个顶点,点
的两个焦点和两个顶点,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() ,
,![]() .
.
(Ⅰ)求椭圆![]() 的方程和点
的方程和点![]() 的坐标;
的坐标;
(Ⅱ)过点![]() 的直线
的直线![]() 与圆
与圆![]() 相交于
相交于![]() 、
、![]() 两点,过点
两点,过点![]() 与
与![]() 垂直的直线
垂直的直线![]() 与椭圆
与椭圆![]() 相交于另一点
相交于另一点![]() ,求
,求![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com