
已知数集 ,其中
,其中 ,且
,且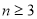 ,若对
,若对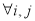 (
(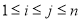 ),
),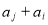 与
与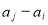 两数中至少有一个属于
两数中至少有一个属于 ,则称数集
,则称数集 具有性质
具有性质
(1)分别判断数集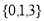 与数集
与数集 是否具有性质
是否具有性质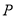 ,说明理由
,说明理由
(2)已知数集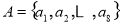 具有性质
具有性质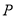 ,判断数列
,判断数列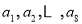 是否为等差数列,若是等差数列,请证明;若不是,请说明理由
是否为等差数列,若是等差数列,请证明;若不是,请说明理由
【解析】
(1)由于3﹣1和3+1都不属于集合{0,1,3},所以该集合不具有性质P;
由于2+0、4+0、6+0、4+2、6﹣2、6﹣4、0﹣0、2﹣2、4﹣4、6﹣6都属于集合{0,2,4,6},
所以该数集具有性质P.…(4分)
(2)∵A={a1,a2,…,a8}具有性质P,所以a8+a8与a8﹣a8中至少有一个属于A,
由0≤a1<a2<…<a8,有a8+a8>a8,故a8+a8∉A,∴0=a8﹣a8∈A,故a1=0.
∵0=a1<a2<…<a8,∴a8+ak>a8,故a8+ak∉A(k=2,3,…,8).
由A具有性质P知,a8﹣ak∈A(k=2,3,…,8).
又∵a8﹣a8<a8﹣a7<…<a8﹣a2<a8﹣a1,
∴a8﹣a8=a1,a8﹣a7=a2,…,a8﹣a2=a7,a8﹣a1=a8,即ai+a9﹣i=a8(i=1,2,…,8).…①
由a2+a7=a8知,a3+a7,a4+a7,…,a7+a7均不属于A,
由A具有性质P,a7﹣a3,a7﹣a4,…,a7﹣a7均属于A,
∴a7﹣a7<a7﹣a6<…<a7﹣a4<a7﹣a3<a8﹣a3 ,
∴a7﹣a7=0,a7﹣a6=a2,a7﹣a5=a3,…,a7﹣a3=a5,即 ai+a8﹣i=a7(i=1,2…7).…②
由①②可知ai=a8﹣a9﹣i=a8﹣(a7﹣ai﹣1) (i=1,2…7,8),
即ai﹣ai﹣1=a8﹣a7(i=2,3,…,8).
故a1,a2,…a8构成等查数列.…(10分)
【解析】
试题分析:(1)根据数集A具有性质P的定义,判断数集{0,1,3}与数集{0,2,4,6}是否具有性质P.
(2)根据数集A={a1,a2…a8}具有性质P,可得ai+a9﹣i=a8 …①,ai+a8﹣i=a7 …②,由①②可知ai=a8﹣a9﹣i=a8﹣(a7﹣ai﹣1),即ai﹣ai﹣1=a8﹣a7,从而得到a1,a2,…a8构成等查数列.
考点:新定义;等差数列与等比数列。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| A、-2 | B、0 |
| C、2 | D、与x有关的一个值 |
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市高三上学期期中考试理科数学试卷(解析版) 题型:选择题
直线 与函数
与函数
 的图象恰有三个公共点,则实数
的图象恰有三个公共点,则实数 的取值范围是( )
的取值范围是( )
(A)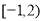 (B)
(B) (C)
(C)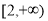 (D)
(D)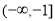
查看答案和解析>>
科目:高中数学 来源:2014-2015学年安徽省淮北市高三第一次模拟考试理科数学试卷(解析版) 题型:选择题
下列命题正确的是( )
A.函数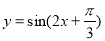 在区间
在区间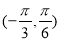 内单调递增
内单调递增
B.函数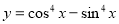 的最小正周期为
的最小正周期为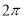
C.函数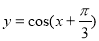 的图像是关于点
的图像是关于点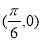 成中心对称的图形
成中心对称的图形
D.函数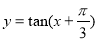 的图像是关于直线
的图像是关于直线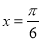 成轴对称的图形
成轴对称的图形
查看答案和解析>>
科目:高中数学 来源:2014-2015学年天津市高三上学期第二次月考文科数学试卷(解析版) 题型:解答题
家政服务公司根据用户满意程度将本公司家政服务员分为两类,其中A类服务员12名,B类服务员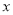 名
名
(1)若采用分层抽样的方法随机抽取20名家政服务员参加技术培训,抽取到B类服务员的人数是16, 求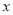 的值
的值
(2)某客户来公司聘请2名家政服务员,但是由于公司人员安排已经接近饱和,只有3名A类家政服务员和2名B类家政服务员可供选择
①请列出该客户的所有可能选择的情况
②求该客户最终聘请的家政服务员中既有A类又有B类的概率来源:学|科|网]
查看答案和解析>>
科目:高中数学 来源:2014-2015学年天津市高三上学期第二次月考文科数学试卷(解析版) 题型:选择题
定义一种运算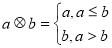 ,令
,令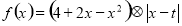 (
(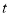 为常数),且
为常数),且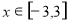 ,则使函数
,则使函数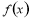 最大值为4的
最大值为4的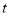 值是( )
值是( )
A.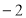 或
或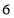 B.
B.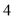 或
或 C.
C.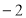 或
或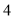 D.
D.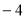 或
或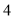
查看答案和解析>>
科目:高中数学 来源:2014-2015学年贵州省高三模拟考试文科数学试卷(解析版) 题型:填空题
给出两个函数性质:
性质1: 是偶函数;
是偶函数;
性质2: 在
在 上是减函数,在
上是减函数,在 上是增函数;
上是增函数;
对于函数:① ;②
;② ; ③
; ③ ,
,
上述两个函数性质都具有的所有函数的序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com