
科目:高中数学 来源: 题型:
等比数列{an}的公比为q,前n项和为Sn,若Sn+1,Sn,Sn+2成等差数列,则公比q为( )
A.q=-2 B.q=1
C.q=-2或q=1 D.q=2或q=-1
查看答案和解析>>
科目:高中数学 来源: 题型:
已知二次函数y=f(x)的图象经过坐标原点,其导函数f ′(x)=2x+2,数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)均在函数y=f(x)的图象上.
(1)求数列{an}的通项公式;
(2)设bn=2n·an,Tn是数列{bn}的前n项和,求Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知p:∃x∈R,mx2+2≤0,q:∀x∈R,x2-2mx+1>0,若p∨q为假命题,则实数m的取值范围是( )
A.m≥1 B.m≤-1
C.m≤-1或m≥1 D.-1≤m≤1
查看答案和解析>>
科目:高中数学 来源: 题型:
对于实数x,规定[x]表示不大于x的最大整数,那么使不等式4[x]2-36[x]+45<0成立的x的取值范围是( )
A.(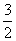 ,
,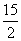 ) B.[2,8]
) B.[2,8]
C.[2,8) D.[2,7]
查看答案和解析>>
科目:高中数学 来源: 题型:
已知抛物线y=(m-1)x2+(m-2)x-1(x∈R).
(1)当m为何值时,抛物线与x轴有两个交点?
(2)若关于x的方程(m-1)x2+(m-2)x-1=0的两个不等实根的倒数平方和不大于2,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
某公司租地建仓库,每月土地占用费y1与仓库到车站的距离成反比,而每月库存货物的运费y2与到车站的距离成正比,如果在距车站10公里处建仓库,这两项费用y1和y2分别为2万元和8万元,那么要使这两项费用之和最小,仓库应建在离车站________公里处.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知动点P(x,y)在正六边形的阴影部分(含边界)内运动,如图,正六边形边长为2,若使目标函数z=kx+y(k>0)取得最大值的最优解有无穷多个,则k值为
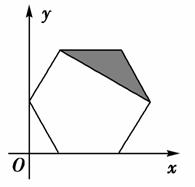
( )
A.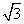 B.
B.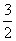
C.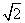 D.4
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com