
已知二次函数y=f(x)的图象经过坐标原点,其导函数f ′(x)=2x+2,数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)均在函数y=f(x)的图象上.
(1)求数列{an}的通项公式;
(2)设bn=2n·an,Tn是数列{bn}的前n项和,求Tn.
(1)设f(x)=ax2+bx,f ′(x)=2ax+b=2x+2,
∴a=1,b=2,f(x)=x2+2x,
∴Sn=n2+2n,
∴当n≥2时,an=Sn-Sn-1=(n2+2n)-[(n-1)2+2(n-1)]=2n+1,
又a1=S1=3,适合上式,∴an=2n+1.
(2)bn=(2n+1)·2n,
∴Tn=3·21+5·22+7·23+…+(2n+1)·2n,
∴2Tn=3·22+5·23+7·24+…+(2n+1)·2n+1,
相减得-Tn=3·21+2·(22+23+…+2n)-(2n+1)·2n+1
=6+2·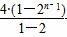 -(2n+1)·2n+1
-(2n+1)·2n+1
=(1-2n)·2n+1-2,
∴Tn=(2n-1)·2n+1+2.


科目:高中数学 来源: 题型:
已知等比数列{an}的公比q=2,它的前9项的平均值等于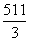 ,若从中去掉一项am,剩下的8项的平均值等于
,若从中去掉一项am,剩下的8项的平均值等于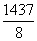 ,则m等于( )
,则m等于( )
A.5 B.6 C.7 D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
小正方形按照下图中的规律排列:
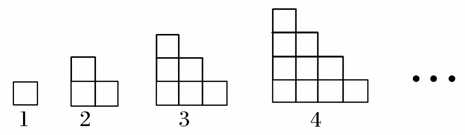
每小图中的小正方形的个数就构成一个数列{an},有以下结论:
①a5=15;②数列{an}是一个等差数列;③数列{an}是一个等比数列;④数列的递推公式为:an=an-1+n(n∈N*),其中正确的为( )
A.①②④ B.①③④
C.①② D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
已知{an}是公差不为0的等差数列,{bn}是等比数列,其中a1=2,b1=1,a2=b2,2a4=b3,且存在常数α、β,使得an=logαbn+β对每一个正整数n都成立,则αβ=________.
查看答案和解析>>
科目:高中数学 来源: 题型:
设等差数列{an}的前n项和为Sn,则a6+a7>0是S9≥S3的( )
A.充分但不必要条件 B.必要但不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
合宁高速公路起自安徽省合肥西郊大蜀山,终于苏皖交界的吴庄,全长133km.假设某汽车从大蜀山进入该高速公路后以不低于60km/h且不高于120km/h的速度匀速行驶到吴庄.已知该汽车每小时的运输成本y(以元为单位)由固定部分和可变部分组成:固定部分为200元;可变部分与速度v(km/h)的平方成正比.当汽车以最快速度行驶时,每小时的运输成本为488元.
(1)把全程运输成本f(v)(元)表示为速度v(km/h)的函数;
(2)汽车应以多大速度行驶才能使全程运输成本最小?最小运输成本为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com