练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．如图，在正方体ABCD-A1B1C1D1中，异面直线A1D与D1C所成的角为（　　）
    A．30°B．45°C．60°D．90°

    分析 连结CB1，ABCD-A1B1C1D1是正方体，A1D∥B1C，异面直线A1D与D1C所成的角为∠B1CD1（或补角），连结B1D1，可得△B1D1C是等边三角形，可得∠B1CD1的大小．

    解答 解：连结CB1，ABCD-A1B1C1D1是正方体，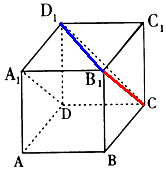
    ∴A1D∥B1C，
    ∴异面直线A1D与D1C所成的角为∠B1CD1（或补角），
    连结B1D1，
    可知B1D1=D1C=B1C，（三条边是平面的对角线）
    ∴△B1D1C是等边三角形，
    ∴∠B1CD1=60°，即异面直线A1D与D1C所成的角为60°．
    故选：C．

    点评 本题考查两条异面直线所成角的大小的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    10．如图是一个几何体的三视图，则这个几何体的体积为（　　）
    A．1B．$\frac{4}{3}$C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．抛掷甲、乙两枚质地均匀且四面上分别标有1，2，3，4的正四面体，其底面落于桌面，记所得的数字分别为x，y，则$\frac{x}{y}$为整数的概率是（　　）
    A．$\frac{1}{2}$B．$\frac{1}{3}$C．$\frac{1}{4}$D．$\frac{1}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知函数f（x）=-x3+12x+m．
    （1）若x∈R，求函数f（x）的极大值与极小值之差；
    （2）若函数y=f（x）有三个零点，求m的取值范围；
    （3）当x∈[-1，3]时，f（x）的最小值为-2，求f（x）的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．某校从参加高三年级学业水平考试的学生中抽出50名学生，并统计了他们的数学成绩（成绩均为整数且满分为150分），其样本频率分布表如下（部分数据丢失）：
    分组频数频率
    [30，50）20.04
    [50，70）30.06
    [70，90）14P1
    [90，110）150.30
    [110，130）xP2
    [130，150）40.08
    合计501
    （Ⅰ）分别求出上表中的x；P1和P2的大小
    （Ⅱ）估计成绩在120分以上学生的比例；
    （Ⅲ）为了帮助成绩差的学生提高数学成绩，学校决定成立“二帮一”小组，即从成绩[130，150）中选两位同学，共同帮助[30，50）中的某一位同学．已知甲同学的成绩为42分，乙同学的成绩为135分，求甲、乙两同学恰好被安排在同一小组的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．下列四个说法：
    ①“x＞2”是“$\frac{1}{x}＜\frac{1}{2}$”的充分不必要条件；
    ②命题“设a，b∈R，若a+b≠6，则a≠3或b≠3”是一个假命题；
    ③命题p：存在x0∈R，使得x02+x0+1＜0，则￢p：任意x∈R都有x2+x+1≥0
    ④一个命题的否命题为真，则它的逆命题一定为真
    其中正确的是（　　）
    A．①④B．②④C．①③④D．①③

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．从集合{1，2，3，5，11}中有放回地任取2次元素分别作为直线Ax+By=0中的A、B，则该直线恰好为坐标系角平分线的概率是（　　）
    A．$\frac{1}{25}$B．$\frac{1}{5}$C．$\frac{1}{2}$D．$\frac{2}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．如图茎叶图记录了甲、乙两组各四名同学的植树棵数，乙组记录中有一个数据模糊，无法确认，在图中以x表示
    附：方差S2=$\frac{1}{n}$[（x1-x）2+（x2-x）2+…+（xn-$\overline{x}$）2]，其中$\overline{x}$为x1，x2，…，xn的平均数
    （1）如果x=8，求乙组同学植树棵数的平均数和方差；
    （2）如果x=9，分别从甲、乙两组中随机选取一名同学，求这两名同学的植树总棵数为19的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．有5条长度分别为1，3，5，6，7的线段，从中任意取出3条，则所取3条线段可以构成三角形的概率为0.4．

    查看答案和解析>>

    同步练习册答案