
【题目】已知平面上一动点A的坐标为![]() .
.
(1)求点A的轨迹E的方程;
(2)点B在轨迹E上,且纵坐标为![]() .
.
(i)证明直线AB过定点,并求出定点坐标;
(ii)分别以A,B为圆心作与直线![]() 相切的圆,两圆公共弦的中点为H,在平面内是否存在定点P,使得
相切的圆,两圆公共弦的中点为H,在平面内是否存在定点P,使得![]() 为定值?若存在,求出点P坐标;若不存在,请说明理由.
为定值?若存在,求出点P坐标;若不存在,请说明理由.
【答案】(1)![]() (2)(i)证明见解析;定点
(2)(i)证明见解析;定点![]() (ii)存在;点
(ii)存在;点![]()
【解析】
(1)设动点A的坐标为![]() ,根据A的坐标为
,根据A的坐标为![]() ,坐标对应相等,消去参数t即可.
,坐标对应相等,消去参数t即可.
(2)(i)根据点B在轨迹E上,且纵坐标为![]() ,得到点B的坐标为
,得到点B的坐标为![]() ,再分
,再分![]() 和
和![]() 两种情况与点A用点斜式方程求解.(ii)根据圆A,B与直线
两种情况与点A用点斜式方程求解.(ii)根据圆A,B与直线![]() 相切,分别表示圆A,圆B的方程,然后两圆方程相减得到公共弦所在直线方程,将
相切,分别表示圆A,圆B的方程,然后两圆方程相减得到公共弦所在直线方程,将![]() ,
,![]() 坐标代入并整理,根据H是该直线与(i)中直线AB的交点,两个方程相乘即可.
坐标代入并整理,根据H是该直线与(i)中直线AB的交点,两个方程相乘即可.
(1)设动点A的坐标为![]() ,
,
因为A的坐标为![]() ,
,
所以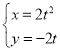 ,
,
消去参数t得:![]() ;
;
(2)(i)因为点B在轨迹E上,且纵坐标为![]() ,
,
所以点B的坐标为![]() ,
,
当![]() 时,直线AB的方程为
时,直线AB的方程为![]() ;
;
当![]() 时,直线AB的斜率为
时,直线AB的斜率为![]() ,
,
所以直线AB的方程为![]() ,
,
整理得![]() ,所以直线AB过定点
,所以直线AB过定点![]() ;
;
(ii)因为A的坐标为![]() ,且圆A与直线
,且圆A与直线![]() 相切,
相切,
所以圆A的方程为![]() ,
,
同理圆B的方程为![]() ,
,
两圆方程相减得![]() ,
,
将![]() ,
,![]() 带入并整理得
带入并整理得![]()
![]() ①,
①,
由(i)可知直线AB的方程为![]()
![]() ②,
②,
因为H是两条直线的交点,
所以两个方程相乘得![]() ,
,
整理得![]() ,即点H的轨迹是以
,即点H的轨迹是以![]() 为圆心,
为圆心,
![]() 为半径的圆,所以存在点
为半径的圆,所以存在点![]() ,满足
,满足![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】我国的西气东输工程把西部的资源优势变为经济优势,实现了气能源需求与供给的东西部衔接,工程建设也加快了西部及沿线地区的经济发展输气管道工程建设中,某段管道铺设要经过一处峡谷,峡谷内恰好有一处直角拐角,水平横向移动输气管经过此拐角,从宽为![]() 米峡谷拐入宽为
米峡谷拐入宽为![]() 米的峡谷.如图所示,位于峡谷悬崖壁上两点
米的峡谷.如图所示,位于峡谷悬崖壁上两点![]() 、
、![]() 的连线恰好经过拐角内侧顶点
的连线恰好经过拐角内侧顶点![]() (点
(点![]() 、
、![]() 、
、![]() 在同一水平面内),设
在同一水平面内),设![]() 与较宽侧峡谷悬崖壁所成角为
与较宽侧峡谷悬崖壁所成角为![]() ,则
,则![]() 的长为________(用
的长为________(用![]() 表示)米.要使输气管顺利通过拐角,其长度不能低于________米.
表示)米.要使输气管顺利通过拐角,其长度不能低于________米.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=n2+pn,且a4,a7,a12成等比数列.
(1)求数列{an}的通项公式;
(2)若bn![]() ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校李老师本学期任高一A班、B班两个班数学课教学,两个班都是50个学生,下图反映的是两个班在本学期5次数学检测中的班级平均分对比,根据图表信息,下列不正确的结论是( )

A. A班的数学成绩平均水平好于B班
B. B班的数学成绩没有A班稳定
C. 下次B班的数学平均分高于A班
D. 在第一次考试中,A、B两个班总平均分为78分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是无穷数列,若存在正整数k,使得对任意
是无穷数列,若存在正整数k,使得对任意![]() ,均有
,均有![]() ,则称
,则称![]() 是间隔递增数列,k是
是间隔递增数列,k是![]() 的间隔数,下列说法正确的是( )
的间隔数,下列说法正确的是( )
A.公比大于1的等比数列一定是间隔递增数列
B.已知![]() ,则
,则![]() 是间隔递增数列
是间隔递增数列
C.已知![]() ,则
,则![]() 是间隔递增数列且最小间隔数是2
是间隔递增数列且最小间隔数是2
D.已知![]() ,若
,若![]() 是间隔递增数列且最小间隔数是3,则
是间隔递增数列且最小间隔数是3,则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电讯企业为了了解某地区居民对电讯服务质量评价情况,随机调查100 名用户,根据这100名用户对该电讯企业的评分,绘制频率分布直方图,如图所示,其中样本数据分组为![]() ,
,![]() ,……
,……![]() .
.
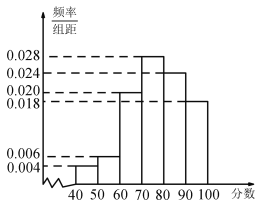
(1)估计该地区用户对该电讯企业评分不低于70分的概率,并估计对该电讯企业评分的中位数;
(2)现从评分在![]() 的调查用户中随机抽取2人,求2人评分都在
的调查用户中随机抽取2人,求2人评分都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年11月26日,联合国教科文组织宣布3月14日为“国际数学日”(昵称:![]() ),2020年3月14日是第一个“国际数学日”.圆周率
),2020年3月14日是第一个“国际数学日”.圆周率![]() 是圆的周长与直径的比值,是一个在数学及物理学中普遍存在的数学常数.
是圆的周长与直径的比值,是一个在数学及物理学中普遍存在的数学常数.![]() 有许多奇妙性质,如莱布尼兹恒等式
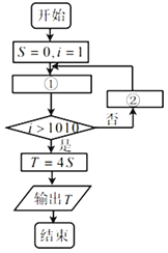
有许多奇妙性质,如莱布尼兹恒等式![]() ,即为正奇数倒数正负交错相加等.小红设计了如图所示的程序框图,要求输出的
,即为正奇数倒数正负交错相加等.小红设计了如图所示的程序框图,要求输出的![]() 值与
值与![]() 非常近似,则①、②中分别填入的可以是( )
非常近似,则①、②中分别填入的可以是( )
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com