
已知下列各组命题,其中p是q的充分必要条件的是________.
①p:m≤-2或m≥6;q:y=x2+mx+m+3有两个不同的零点
②p: =1;q:y=f(x)是偶函数
=1;q:y=f(x)是偶函数
③p:cos α=cos β;q:tan α=tan β
④p:A∩B=A;q:A⊆U,B⊆U,∁UB⊆∁UA
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
已知△ABC的内角B满足2cos 2B-8cos B+5=0,若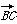 =a,
=a,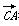 =b且a,b满足:a·b=-9,|a|=3,|b|=5,θ为a,b的夹角.
=b且a,b满足:a·b=-9,|a|=3,|b|=5,θ为a,b的夹角.
(1)求角B;
(2)求sin(B+θ).
查看答案和解析>>
科目:高中数学 来源: 题型:
下列判断中正确的是( )
A.△ABC中,a=7,b=14,A=30°,有两解
B.△ABC中,a=30,b=25,A=150°,有一解
C.△ABC中,a=6,b=9,A=45°,有两解
D.△ABC中,b=9,c=10,B=60°,无解
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com