
已知函数 ,
,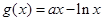 ,其中
,其中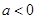 ,
,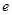 为自然对数的底数.
为自然对数的底数.
(1)若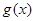 在
在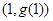 处的切线
处的切线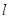 与直线
与直线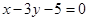 垂直,求
垂直,求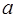 的值;
的值;
(2)求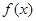 在
在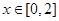 上的最小值;
上的最小值;
(3)试探究能否存在区间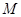 ,使得
,使得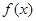 和
和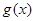 在区间
在区间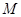 上具有相同的单调性?若能存在,说明区间
上具有相同的单调性?若能存在,说明区间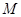 的特点,并指出
的特点,并指出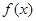 和
和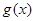 在区间
在区间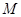 上的单调性;若不能存在,请说明理由.
上的单调性;若不能存在,请说明理由.
(1)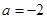 ;(2)
;(2)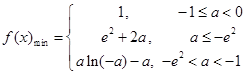
(3)当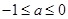 时,不能存在区间
时,不能存在区间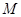 ,使得
,使得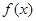 和
和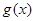 在区间
在区间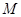 上具有相同的单调性;当
上具有相同的单调性;当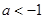 时,存在区间
时,存在区间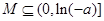 ,使得
,使得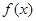 和
和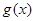 在区间
在区间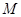 上均为减函数.
上均为减函数.
解析试题分析:(1)切点处的导数值,即为切线的斜率,根据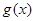 在
在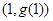 处的切线
处的切线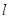 与直线
与直线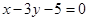 垂直,斜率乘积为
垂直,斜率乘积为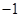 ,建立
,建立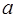 的方程;
的方程;
(2)遵循求导数、求驻点、讨论区间单调性、确定极值(最值);
(3)求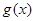 的定义域为
的定义域为 ,及导数
,及导数 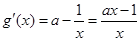 .
.
根据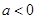 时,
时,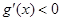 ,知
,知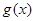 在
在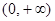 上单调递减.
上单调递减.
重点讨论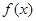 的单调性.
的单调性.
注意到其驻点为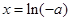 ,故应讨论:
,故应讨论:
①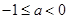 , ②
, ②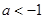 的情况,作出判断.
的情况,作出判断.
综上,当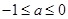 时,不能存在区间
时,不能存在区间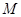 ,使得
,使得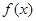 和
和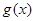 在区间
在区间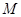 上具有相同的单调性;当
上具有相同的单调性;当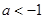 时,存在区间
时,存在区间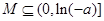 ,使得
,使得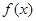 和
和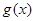 在区间
在区间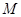 上均为减函数.
上均为减函数.
试题解析:(1)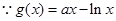 ,
,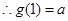 ,
,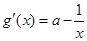
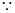
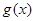 在
在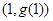 处的切线
处的切线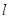 与直线
与直线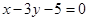 垂直,
垂直,
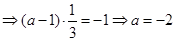 3分
3分
(2)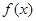 的定义域为
的定义域为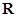 ,且
,且 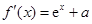 .
.
令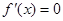 ,得
,得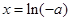 . 4分
. 4分
若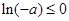 ,即
,即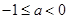 时,
时,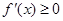 ,
,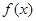 在
在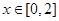 上为增函数,
上为增函数,
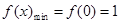 ;5分
;5分
若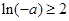 ,即
,即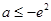 时,
时,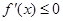 ,
,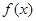 在
在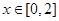 上为减函数,
上为减函数,
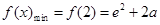 ; 6分
; 6分
若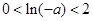 ,即
,即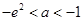 时,
时,
由于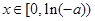 时,
时,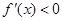 ;
;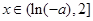 时,
时,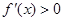


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:解答题
已知函数f(x)=x3-3ax2+3x+1.
(1)设a=2,求f(x)的单调区间;
(2)设f(x)在区间(2,3)中至少有一个极值点,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
根据统计资料,某工艺品厂的日产量最多不超过20件,每日产品废品率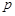 与日产量
与日产量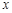 (件)之间近似地满足关系式
(件)之间近似地满足关系式 (日产品废品率
(日产品废品率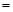
 ).已知每生产一件正品可赢利2千元,而生产一件废品则亏损1千元.(该车间的日利润
).已知每生产一件正品可赢利2千元,而生产一件废品则亏损1千元.(该车间的日利润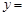 日正品赢利额
日正品赢利额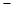 日废品亏损额)
日废品亏损额)
(1)将该车间日利润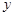 (千元)表示为日产量
(千元)表示为日产量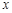 (件)的函数;
(件)的函数;
(2)当该车间的日产量为多少件时,日利润最大?最大日利润是几千元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知某工厂生产 件产品的成本为
件产品的成本为 (元),
(元),
问:(1)要使平均成本最低,应生产多少件产品?
(2)若产品以每件500元售出,要使利润最大,应生产多少件产品?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com