Question

10．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点分别为E，F，以OF（O为坐标原点）为直径的圆C角双曲线于A，B两点，AE与圆C相切，则该双曲线的离心率为（　　）

• A． $\frac{\sqrt{2}+3\sqrt{6}}{2}$
• B． $\frac{2\sqrt{2}+\sqrt{6}}{2}$
• C． $\frac{3\sqrt{2}+\sqrt{6}}{2}$
• D． $\frac{3\sqrt{2}+2\sqrt{6}}{2}$

Answer 1

分析 根据直线和圆相切以及点A在双曲线上，结合余弦定理以及双曲线的定义建立关于a，c的方程进行求解即可．

解答 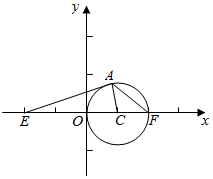解：由椭圆的方程得E（-c，0），F（c，0），C（$\frac{c}{2}$，0），
∵AE与圆C相切，同时A是圆与双曲线的交点，∴A实数切点，则AE⊥AC，
则AC=$\frac{c}{2}$，CE=c+$\frac{c}{2}$=$\frac{3}{2}$c，
则AE=$\sqrt{（\frac{3c}{2}）^{2}-（\frac{c}{2}）^{2}}$=$\sqrt{2}$c，
cos∠ACE=$\frac{A{C}^{2}+C{E}^{2}-A{E}^{2}}{2AC•CE}$=$\frac{\frac{{c}^{2}}{4}+\frac{9{c}^{2}}{4}-2{c}^{2}}{2×\frac{c}{2}×\frac{3c}{2}}$=$\frac{1}{3}$，
则cos∠ACF=-cos∠ACE=-$\frac{1}{3}$，
则AF²=AC²+CF²-2AC•CFcos∠ACF=$\frac{{c}^{2}}{4}$+$\frac{{c}^{2}}{4}$+2×$\frac{c}{2}$×$\frac{c}{2}$×$\frac{1}{3}$=$\frac{2}{3}$c²，
则AF=$\sqrt{\frac{2}{3}}$c=$\frac{\sqrt{6}}{3}$c，
∵点A在双曲线上，
∴AE-AF=2a，
即$\sqrt{2}$c-$\frac{\sqrt{6}}{3}$c=2a，
即$\frac{3\sqrt{2}-\sqrt{6}}{3}$c=2a，
则e=$\frac{c}{a}$=$\frac{6}{3\sqrt{2}-\sqrt{6}}$=$\frac{6（3\sqrt{2}+\sqrt{6}）}{18-6}$=$\frac{3\sqrt{2}+\sqrt{6}}{2}$，
故选：C．

点评 本题主要考查双曲线离心率的计算，根据直线和圆相切以及双曲线的定义，余弦定理求出相应的边长是解决本题的关键．综合性较强，有一定的难度．