
分析 连接BD,由已知,利用余弦定理可求BD的值,进而可求cos∠ADB的值,利用两角差的余弦函数公式可求cos∠CDB的值,进而利用余弦定理即可得解BC的值.
解答 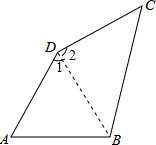 解:如图,连接BD,由AB=8,AD=5,∠A=60°,
解:如图,连接BD,由AB=8,AD=5,∠A=60°,
则由余弦定理BD=$\sqrt{A{B}^{2}+A{D}^{2}-2AB•AD•cosA}$=$\sqrt{64+25-2×8×5×\frac{1}{2}}$=7,
可得:cos∠1=$\frac{A{D}^{2}+B{D}^{2}-A{B}^{2}}{2AD•BD}$=$\frac{25+49-64}{2×5×7}$=$\frac{1}{7}$,可得:sin∠1=$\sqrt{1-co{s}^{2}∠1}$=$\frac{4\sqrt{3}}{7}$,
∵CD=3$\sqrt{3}$,∠D=150°,
∴cos∠2=cos(150°-∠2)=(-$\frac{\sqrt{3}}{2}$)×$\frac{1}{7}$+$\frac{1}{2}×\frac{4\sqrt{3}}{7}$=$\frac{3\sqrt{3}}{14}$,
∴BC=$\sqrt{C{D}^{2}+B{D}^{2}-2BD•CD•cos∠2}$=$\sqrt{27+49-2×7×3\sqrt{3}×\frac{3\sqrt{3}}{14}}$=7.
故答案为:7.
点评 本题考查了余弦定理、两角差的余弦函数公式在解三角形中的应用,根据已知条件求cos∠CDB的值是解题关键,属于中档题.


科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
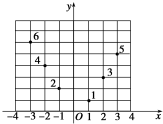 如图所示,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列{an}(n∈N*)的前12项,如表所示.
如图所示,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列{an}(n∈N*)的前12项,如表所示.| a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | a11 | a12 |
| x1 | y1 | x2 | y2 | x3 | y3 | x4 | y4 | x5 | y5 | x6 | y6 |
| A. | 1 003 | B. | 1 005 | C. | 1 006 | D. | 2 010 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | $-\frac{1}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 该数列一定是等差数列 | B. | 该数列一定不是等差数列 | ||
| C. | 该数列不一定是等差数列 | D. | 以上结论都不正确 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com