
分析 首先由已知等式求得a值,然后利用三角恒等变换sin2x=cosx求出所有根的个数,最后利用排列组合的思想求得满足条件的有序实数组.
解答 解:∵对任意实数x都有2sin(3x-$\frac{π}{3}$)=asin(bx+c),∴|a|=2,
若a=2,则方程等价于sin(3x-$\frac{π}{3}$)=sin(bx+c),则函数的周期相同,
若b=3,此时c=$\frac{5π}{3}$;若b=-3,此时c=$\frac{4π}{3}$;
若a=-2,则方程等价于sin(3x-$\frac{π}{3}$)=-sin(bx+c)=sin(-bx-c),
若b=-3,此时c=$\frac{π}{3}$;若b=3,此时c=$\frac{2π}{3}$.
综上,满足条件的数组(a,b,c,)为(2,3,$\frac{5π}{3}$),(2,-3,$\frac{4π}{3}$),
(-2,-3,$\frac{π}{3}$),(-2,3,$\frac{2π}{3}$)共4组.
而当sin2x=cosx时,2sinxcosx=cosx,得cosx=0或sinx=$\frac{1}{2}$,
∴x=$\frac{π}{2}$+kπ或x=$\frac{π}{6}$+2kπ,k∈Z
又∵x∈[0,3π],∴x=$\frac{π}{2},\frac{3π}{2},\frac{5π}{2},\frac{π}{6},\frac{13π}{6},\frac{5π}{6},\frac{17π}{6}$.
∴满足条件的有序数组(a,b,c,d)共有4×7=28.
故答案为28.
点评 本题考查三角函数的周期性、三角函数的恒等变换及三角函数的图象和性质,考查渗透转化与化归思想方法,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
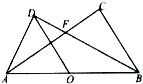 如图,△ABC与△ABD都是以AB为斜边的直角三角形,O为线段AB上一点,BD平分∠ABC,且OD∥BC.
如图,△ABC与△ABD都是以AB为斜边的直角三角形,O为线段AB上一点,BD平分∠ABC,且OD∥BC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,\frac{{\sqrt{e}}}{e}-8]$ | B. | $[\frac{{\sqrt{e}}}{e}-8,+∞)$ | C. | $[\sqrt{2},e)$ | D. | $(-\frac{{\sqrt{3}}}{3},\frac{e}{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 6 | C. | -4或10 | D. | 0或6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com